Взаимное расположение двух плоскостей в пространстве. Признаки параллельности двух плоскостей

Взаимное расположение двух плоскостей в пространстве. Признаки параллельности двух плоскостей

Признаки параллельности плоскостей

Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся плоскости		Две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия.
Две параллельные плоскости		Две плоскости называют параллельными, если они не имеют общих точек.

Признаки параллельности двух плоскостей

Первый признак параллельности двух плоскостей. Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Доказательство. Рассмотрим рисунок 1, на котором изображены плоскости α и β

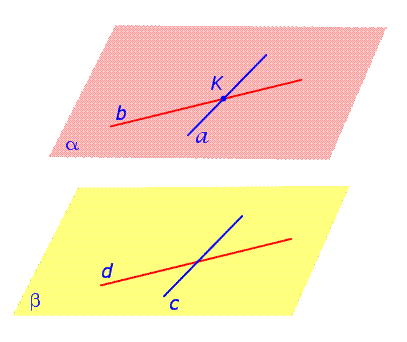
Рис.1

Прямые a и b лежат в плоскости α и пересекаются в точке K. Прямые c и d лежат в плоскости β и параллельны прямым a и b соответственно.

Будем доказывать первый признак параллельности двух плоскостей методом «от противного». Для этого предположим, что плоскости α и β не параллельны. Следовательно, плоскости α и β должны пересекаться, причём пересекаться по некоторой прямой. Обозначим прямую линию, по которой пересекаются плоскости α и β буквой l (рис.2) и воспользуемся признаком параллельности прямой и плоскости.

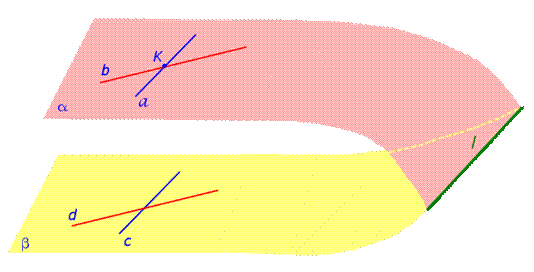
Рис.2

Плоскость α проходит через прямую a, параллельную прямой c, и пересекает плоскость β по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые a и l параллельны. В то же время плоскость α проходит через прямую b, параллельную прямой d, и пересекает плоскость β по прямой l. Отсюда, в силу признака параллельности прямой и плоскости, заключаем, что прямые b и l параллельны. Таким образом, мы получили, что на плоскости α через точку K проходят две прямые, а именно, прямые a и b, которые параллельны прямой l. Полученное противоречие с аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости α и β пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.

Второй признак параллельности двух плоскостей. Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.

Доказательство. Рассмотрим рисунок 3, на котором изображены плоскости α и β.

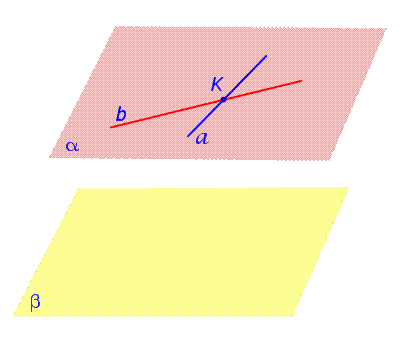
Рис.3

На этом рисунке также изображены прямые a и b, которые лежат в плоскости α и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости β. Требуется доказать, что плоскости α и β параллельны.

Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы его оставляем читателю в качестве полезного упражнения.

⇐ Предыдущая 1 2 34