Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение.Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

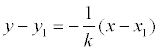
Расстояние от точки до прямой

Теорема.Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как:

Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

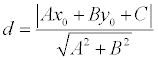Помним, что прямая бесконечная…….

Углы между прямыми

Пример. Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k ₁ = -3; k ₂ = 2; tgφ = 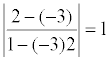; φ= π /4.

Пример. Показать, что прямые

3х – 5у + 7 = 0 и 10х + 6у – 3 = 0

перпендикулярны.

Решение. Находим: k ₁ = 3/5, k₂ = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника

А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение. Находим уравнение стороны АВ: ;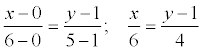

получ 4 x = 6 y – 6; 2 x – 3 y + 3 = 0;

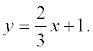
Искомое уравнение высоты имеет вид:

Ax + By + C = 0 или y = kx + b .

k = 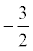. Тогда y = .

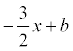Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: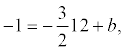

откуда b = 17. Итого: .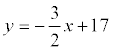

Ответ: 3x + 2y – 34 = 0.