
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнение прямой на плоскости. Уравнение прямой по точке и вектору нормали. Определение.В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.. Уравнение прямой, проходящей
Уравнение прямой на плоскости
Определение.Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общимуравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и вектору нормали
Определение.В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору  (3, -1).
(3, -1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно, С = -1. Итого: искомое уравнение:
3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки
Пусть на плоскости заданы две точки  (
( 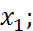
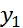 ) и
) и
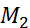 (
( 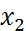 ,
, 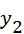 ), тогда уравнение прямой, проходящей через эти точки:
), тогда уравнение прямой, проходящей через эти точки:
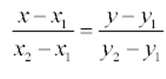
Полученное уравнение называется КАНОНИЧЕСКИМ УРАВНЕНИЕМ ПРЯМОЙ на плоскости.Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. Знаменатели являются координатами направляющего вектора прямой(Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.) т.е.
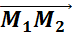 (
( 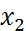 -
- 
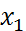 ;
; 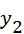 -
- 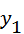 )
)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|