Уравнение прямой с угловым коэффициентом

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Уравнение прямой с угловым коэффициентом

Можно преобразовать записанное выше уравнение прямой:

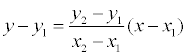
если х₁ ≠ х₂ и х = х₁ , если х₁ = х₂ .

Дробь 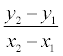= k называется угловым коэффициентомпрямой. Уравнение прямой с угловым коэффициентом примет вид:

y = kx +b

b –свободный член.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем

Уравнение общего вида:

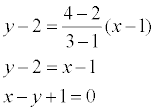
Уравнение прямой с угловым коэффициентом:

y = x +1

Уравнение прямой по точке и направляющему вектору

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Определение.Каждый ненулевой вектор ( α1 , α2 ), компоненты которого удовлетворяют условию Аα1 + Вα2 = 0

называется направляющим вектором прямой

Ах + Ву + С = 0.

Пример. Найти уравнение прямой с направляющим вектором 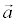(1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0,или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

х + у ̶ 3 = 0

Угол между прямыми на плоскости

Определение.Если заданы две прямые y = k₁ x + b₁ , y = k ₂x + b₂ , то острый угол между этими прямыми будет определяться как

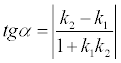Две прямые параллельны, если k₁ = k₂ . Две прямые перпендикулярны, если k₁ = -1/ k₂ .

Теорема.Прямые Ах + Ву + С = 0 и А ₁ х + В₁ у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = λА, В₁ = λВ. Если еще и С₁ = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

⇐ Предыдущая 123 Следующая ⇒