
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Разложение функций в степенные ряды. Ряд Тейлора.
3. Разложение функций в степенные ряды. Ряд Тейлора.
Ряд 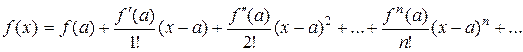
называется рядом Тейлора для функции f(x). В частности, при a = 0 ряд принимает вид
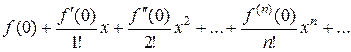
Этот ряд называют рядом Маклорена для функции f(x).
Разложение некоторых элементарных функций в ряды Тейлора и Маклорена.
1) Разложение в степенной ряд функции  .
.
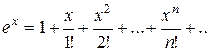 - данное разложение имеет место на всей числовой оси.
- данное разложение имеет место на всей числовой оси.
2) Разложение в степенной ряд функции f(x) = sinx.
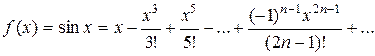
3) Если f(x) = cosx, то
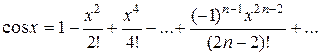 - это разложение справедливо на (-¥ ; +¥).
- это разложение справедливо на (-¥ ; +¥).
4) Биномиальный ряд. 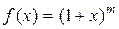 .
.
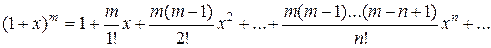
Это разложение имеет место при m ³ 0, если -1 £ x £ 1,
при -1 < m <0, если -1< x £ 1,
при m £ -1, если -1< x < 1.
5) Разложение в степенной ряд функции y = lnx.
При x = 0 функция lnx неопределенна, поэтому её нельзя разложить по степеням x, т.е. ряд Маклорена. Разложим функцию y = lnx в ряд Тейлора по степеням x - 1.
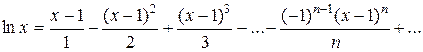 ,
, 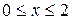
В частности,
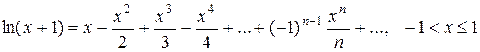
Пример 11.Разложить в степенной ряд функцию 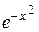 .
.
Решение. Положим 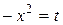 , тогда
, тогда 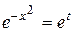 . Тогда
. Тогда 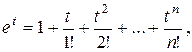
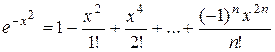 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|