
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Требования к содержанию отчета по работе
Требования к содержанию отчета по работе
Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
Контрольные вопросы (Задания для самопроверки качества освоенных результатов обучения):
- понятие случайной величины
- законом распределения случайной величины
- формула математического ожидания и дисперсии случайной величины
Приложение
Задание 1. Задает ли закон распределения дискретной случайной величины данная таблица
1)
| X | |||||
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
2)
| X | |||||
| P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
3)
| X | |||||
| P | 0,13 | 0,17 | 0,3 | 0,37 | 0,68 |
4)
| X | |||||
| P | 0,2 | 0,3 | 0,11 | 0,13 | 0,47 |
5)
| X | |||||
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
6)
| X | |||||
| P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
7)
| X | |||||
| P | 0,13 | 0,17 | 0,3 | 0,37 | 0,68 |
8)
| X | |||||
| P | 0,2 | 0,3 | 0,11 | 0,13 | 0,47 |
9)
| X | |||||
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
10)
| X | |||||
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
Задание 2. Дискретная случайная величина имеет закон распределения. Найти неизвестную вероятность.
1)
| X | |||||
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
2)
| X | |||||
| P | 0,15 | 0,16 | P3 | 0,5 | 0,07 |
3)
| X | |||||
| P | 0,3 | P2 | 0,2 | 0,29 | 0,1 |
4)
| X | |||||
| P | 0,16 | P2 | 0,15 | 0,07 | 0,5 |
5)
| X | |||||
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
6)
| X | |||||
| P | 0,15 | 0,16 | P3 | 0,5 | 0,07 |
7)
| X | |||||
| P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
8)
| X | |||||
| P | 0,3 | P2 | 0,2 | 0,29 | 0,1 |
9)
| X | |||||
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
10)
| X | |||||
| P | 0,3 | P2 | 0,2 | 0,29 | 0,1 |
Задание 3.
1) В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
2)В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
3) В партии из 10 деталей имеется 7 стандартных. Берут 2 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
4) В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
5) В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
6)В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
7) В партии из 10 деталей имеется 7 стандартных. Берут 2 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
8) В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
9) В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
10) В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
Задание 4.
Вариант1
1. Случайная величина X распределена по закону:
| –1 | |||
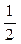
| 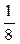
| 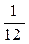
| 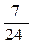
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. В лотерее разыгрывается 20000 билетов. Найдите математическое ожидание и дисперсию числа выигрышных билетов, если каждый билет может выигрышным с вероятностью 0,3.
Вариант 2
1. Случайная величина X распределена по закону:
| 0 | |||
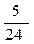
| 
| 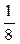
| 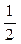
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. В магазин поступила партия из 50 коробок с обувью черного и коричневого цвета. Найдите математическое ожидание и дисперсию числа коробок с обувью коричневого цвета, если вероятность того, что обувь будет коричневого цвета равна 0,2.
Вариант 3
1. Случайная величина X распределена по закону:
| –1 | ||
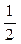
| 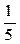
| 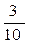
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа не взошедших семян из 800 посеянных семян данного растения, если каждое из семян может не взойти с вероятностью 0,01.
Вариант 4
1. Случайная величина X распределена по закону:
| –1 | |||
| 0,1 | 0,2 | 0,3 | 0,4 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа студентов, которые не сдадут экзамен, в группе из 30 человек, если каждый студент может не сдать экзамен с вероятностью 0,4.
Вариант 5
1. Случайная величина X распределена по закону:
| –2 | –1 | ||
| 0,2 | 0,1 | 0,2 | 0,5 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. В урне находятся всего 100 белых и чёрных шаров. Найдите математическое ожидание и дисперсию числа белых шаров, если вероятность того, что шар будет белым равна 0,02.
Вариант 6
1. Случайная величина X распределена по закону:
| 1 | ||
| 0,07 | 0,03 | 0,9 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа нестандартных ламп в партии из 300 ламп, если каждая лампа может оказаться нестандартной с вероятностью 0,07.
Вариант 7
1. Случайная величина X распределена по закону:
| –1 | ||
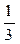
| 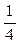
| 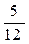
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа фальшивых билетов, купленных на самолёт, в партии из 150 билетов, если каждый билет может оказаться фальшивым с вероятностью 0,004.
Вариант 8
1. Случайная величина X распределена по закону:
| 0,4 | 0,5 | 0,1 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 7000 деталей, если каждая деталь может оказаться со знаком качества с вероятностью 0,8.
Вариант 9
1. Случайная величина X распределена по закону:
| –1 | ||
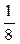
| 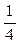
| 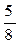
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа поддельных медицинских препаратов в партии из 126 препаратов, если каждый препарат может быть поддельным с вероятностью 0,06.
Вариант 10
1. Случайная величина X распределена по закону:
| –1 | |||
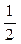
| 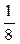
| 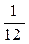
| 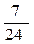
|
2. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 7000 деталей, если каждая деталь может оказаться со знаком качества с вероятностью 0,8.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|