a. Замена переменной в несобственных интегралах 2-го рода

⇐ ПредыдущаяСтр 3 из 3

a. Замена переменной в несобственных интегралах 2-го рода

Пример 13:

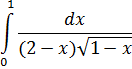
Функция терпит бесконечный разрыв в т. х=1.

Введём замену:

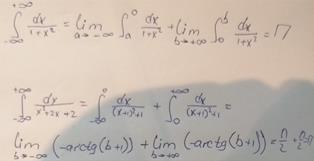
b. Интегрирование по частям в несобственных интегралах 2-го рода

Пример 14:

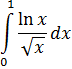
Подынтегральная функция не существует в т. х=0. Имеем несобственный интеграл 2-го рода.

Воспользуемся методом интегрирования по частям.

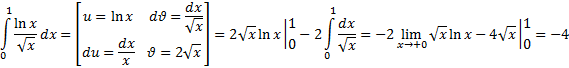
3. Точки разрыва на обоих концах отрезка

Методика решения аналогична решению интегралов с бесконечными пределами: разделить интеграл на два несобственных интеграла.

Пример 15 (№ 2337, Демидович)

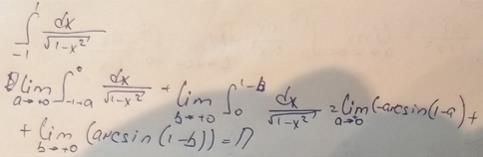
Метод решения несобственного интеграла от четной функции по симметричному относительно нуля отрезку

Пример 16:

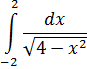
Подынтегральная функция терпит бесконечные разрывы в точках х= -2, х=2. Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.

Интеграл целесообразно споловинить, а результат удвоить.

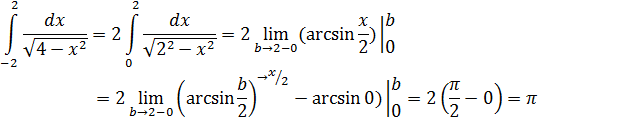
4. Точка разрыва внутри промежутка интегрирования

Рассмотрим пример 17:

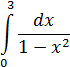
На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке х=1.

Представим несобственный интеграл в виде суммы двух несобственных интегралов:

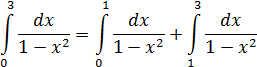
Имеем несобственные интегралы 2-го рода, алгоритм решения которых представлен в пунктах 1 и 2.

⇐ Предыдущая 1 23