
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
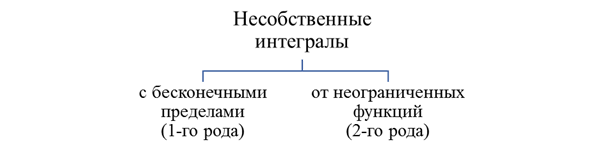
Несобственные интегралы. Несобственные интегралы 1-го рода. a. Обобщение формулы Ньютона-Лейбница. b. Замена переменной. c. Внесение функции под знак дифференциала. d. Интегрирование по частям
Несобственные интегралы
ПММ, 1 курс, 9 группа, Спицын А. С.
Перед решением любого несобственного интеграла важно проверить подынтегральную функцию на непрерывность.
Несобственные интегралы 1-го рода
1. Бесконечный верхний предел интегрирования: 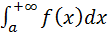
a. Обобщение формулы Ньютона-Лейбница
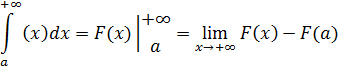
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Найти неопределённый интеграл.
3. Подставить верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.
Пример 1:
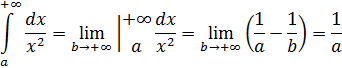
Пример 2 (№ 2338, Демидович):
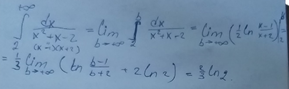
b. Замена переменной
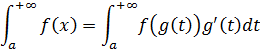
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Ввести замену и преобразовать исходный интеграл согласно формуле.
3. Полученный интеграл вычислить с помощью формулы Ньютона-Лейбница (см. предыдущий пункт)
Пример 3:
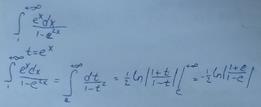
c. Внесение функции под знак дифференциала
Алгоритм аналогичен предыдущим, однако вместо замены переменной при поиске первообразной используем метод внесения функции под знак дифференциала.
Пример 4:

Функция непрерывна на исследуемом отрезке, найдём несобственный интеграл:
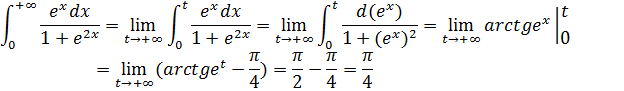
d. Интегрирование по частям
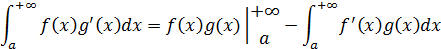
Алгоритм решения:
1. Проверить непрерывность функции на промежутке интегрирования.
2. Применить формулу интегрирования по частям.
3. Вычислить необходимые пределы и несобственные интегралы.
Пример 5:
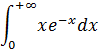
Подынтегральное выражение позволяет применить метод интегрирования по частям:
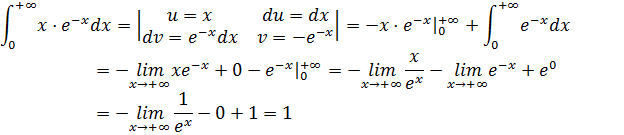
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|