
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
e. Пример несуществования интеграла
e. Пример несуществования интеграла
Пример 6:
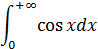
Данного несобственного интеграла не существует, так как
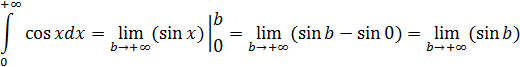
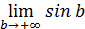
в свою очередь не существует.
2. Бесконечный нижний предел интегрирования: 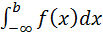
Общий алгоритм:
· найти первообразную (неопределённый интеграл)
· использовать предел при вычислении интеграла
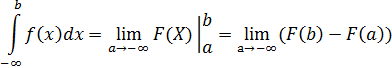
Пример 7:
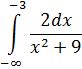
Подынтегральная функция непрерывна на (– ∞; –3]. Найдём несобственный интеграл, используя уже известные методы и устремив нижний предел к – ∞.
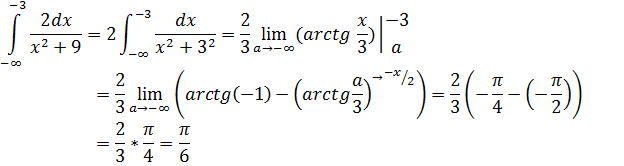
3. Бесконечные пределы интегрирования (и верхний, и нижний): 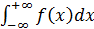
Методика: представить в виде суммы двух несобственных интегралов
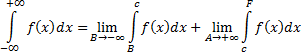
Пример 8 :
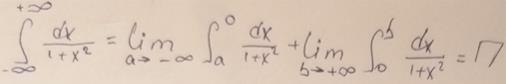
Пример 9:
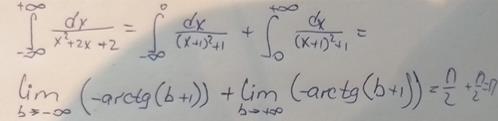
Метод решения несобственного интеграла от четной функции по симметричному относительно нуля отрезку
Пример 10:
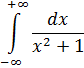
Подынтегральная функция является чётной. В несобственных интегралах с бесконечными пределами (а значит, симметричным интервалом интегрирования) чётностью пользоваться можно. Промежуток выгодно споловинить, а результат – удвоить:
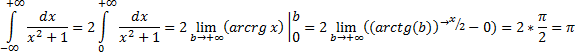
Несобственные интегралы 2-го рода
1. Подынтегральная функция не существует в т. x=a
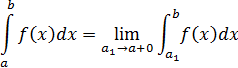
Алгоритм решения:
1. Поверить пределы интегрирования, подставив в подынтегральную функцию.
2. Вычислить неопределённый интеграл, используя известные методы.
3. Подставляем верхний и нижний предел по модифицированной формуле Ньютона-Лейбница, устремив предел к значению а справа.
4. Вычислить полученное выражение.
Пример 11:
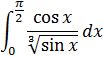
Подынтегральная функция не определена в т. х=0. Следовательно, функция не ограничена в правосторонней окрестности точки х=0.
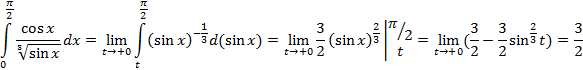
2. Подынтегральная функция не существует в т. x=b
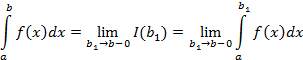
Алгоритм решения аналогичен предыдущему, единственное отличие в стремлении предела к значению b слева.
Пример 12:
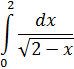
Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому
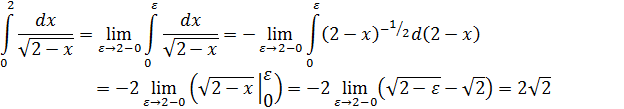
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|