Контакты

Случайная статья

Замена переменных в двойном интеграл

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

4. Замена переменных в двойном интеграл

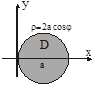Задача. Вычислить ,

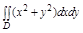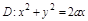
1. Перейдем в полярную систему координат

, ,

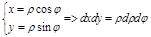
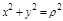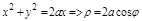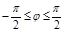
2.

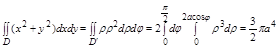
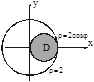
Задача. Вычислить площадь фигуры ограниченной линиями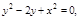

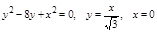
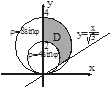Как и в предыдущем случае для достижения правильности области D нам придется рассекать её на три части.

Перейдем к полярной системе координат

,

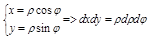
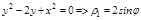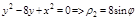
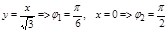
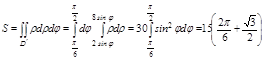
Тройной интеграл

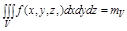
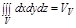
Задача. Вычислить 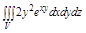, где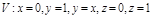

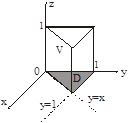1. Область V правильная в направлении оси Oz, а область D правильная во всех направлениях

Замечание. Если направление интегрирование области не имеет значения, надо выбрать то, которое упростит процесс непосредственного вычисление интегралов

а.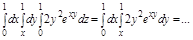

б.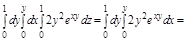

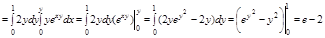
Задача. Вычислить 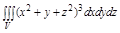, где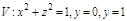

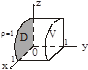1. Данная область V правильная в направлении оси Oz, поэтому спроектируем её в плоскость xOz

2. Перейдем в цилиндрическую систему координат

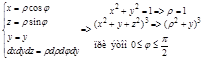
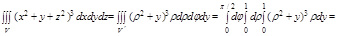
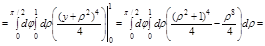
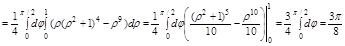
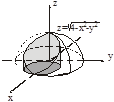Задача. Вычислить объем тела, ограниченного поверхностями , ,

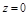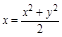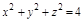
1. Область V в правильная в направлении оси Oz, а область D неправильная во всех направлениях.

2. Перейдем в цилиндрическую систему координат

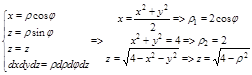
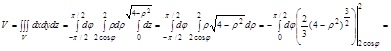
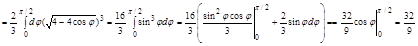
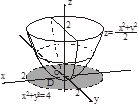
Задача. Вычислить тройной интеграл 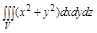, где V: ограничена плоскостью z=2 и параболоидом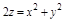

1. Область V правильная в направлении оси Oz в пределах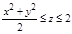

2. Область D, проекция тела V в плоскости xOy, правильная во всех направлениях и представляет окружность, для удобства вычисления перейдем к цилиндрической системе координат:

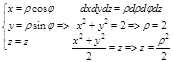Þ D: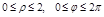

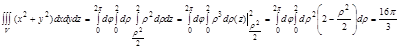
Примечание: 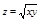- конус.

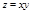- гиперболический параболоид (повернутый)

⇐ Предыдущая 123 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.