
- Р Р‡.МессенРТвЂВВВВжер
- ВКонтакте
- РћРТвЂВВВВнокласснРСвЂВВВВРєРСвЂВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнения вида cosx=a.. Уравнения вида tgx=a.
2. Уравнения вида cosx=a.
Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а.
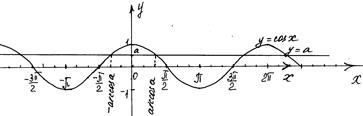
1) Если а<-1 и а> 1, то уравнение cosx=a не имеет решений, так как графики не имеют общих точек.
2) Если -1<a< 1, то уравнение cosx=a имеет бесконечное множество решений.
Найдем все решения cosx=a на промежутке длины 2  так как период косинуса равен 2
так как период косинуса равен 2  .
.
На [0;  ] решением уравнения по определению арккосинуса будет х=arcos a. Учитывая четность функции косинус решением уравнения на [-
] решением уравнения по определению арккосинуса будет х=arcos a. Учитывая четность функции косинус решением уравнения на [-  ;0] будет х=-arcos a.
;0] будет х=-arcos a.
Таким образом решения уравнения cosx=a х=+ arcos a+2  n,
n,
В трех случаях будем пользоваться не общей формулой, а более простыми сотношениями:
Если а=-1, то cosx =-1, x =-  /2+2
/2+2  n
n
Если а=1, то cosx =1, x = 2  n,
n,
Если а=0, то cosx =0. x =  /2+
/2+  n
n
Пример: Решить уравнение cos x =1/2,
Составим формулы решений x=arccos 1/2+ 2  n
n
Вычислим значение arccos1/2.
Подставим найденное значение в формулы решений
X=+  /3+2
/3+2  n, n
n, n 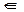 Z.
Z.
2. Уравнения вида tgx=a.
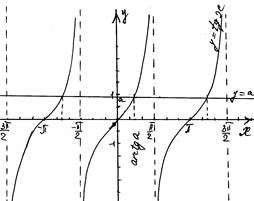
Так как период тангенса равен  , то для того чтобы найти все решения уравнения tgx=a, достаточно найти все решения на любом промежутке длины
, то для того чтобы найти все решения уравнения tgx=a, достаточно найти все решения на любом промежутке длины  . По определению арктангенса решение уравнения на (-
. По определению арктангенса решение уравнения на (-  /2;
/2;  /2) есть arctga. Учитывая период функции все решения уравнения можно записать в виде
/2) есть arctga. Учитывая период функции все решения уравнения можно записать в виде
х= arctg a+  n, n
n, n 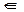 Z.
Z.
Пример: Решите уравнение tg x = 3/3
Составим формулу для решения х= arctg 3/3 +  n, n
n, n 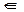 Z.
Z.
Вычислим значение арктангенса arctg 3/3=  /6, тогда
/6, тогда
х=  /6+
/6+  n, n
n, n 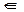 Z.
Z.
Вывод формулы для решения уравнения сtgx=aможно предоставить учащимся.
Пример.
Решить уравнение ctg х = 1.
х = arcсtg 1 +  n, n
n, n 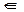 Z,
Z,
х =  /4 +
/4 +  n, n
n, n 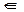 Z.
Z.
В результате изученного материала учащиеся могут заполнить таблицу:
«Решение тригонометрических уравнений».
| уравнение | формулы корней |
| sinx =a | х= ( -1)narcsin a+  n, n n, n 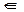 Z. Z.
|
| cosx=a | х=+ arcos a+2  n, n n, n 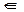 Z. Z.
|
| tgx=a | х= arctg a+  n, n n, n 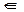 Z. Z.
|
| сtgx=a | х= arcсtg a+  n, n n, n 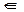 Z. Z.
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|