Определение гармонических колебаний.

Определение гармонических колебаний.

Величина Х (физическая величина) считается гармонически колеблющейся (изменяющейся), если 2-я производная 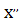от этой величины пропорциональна самой этой величине х, взятой с обратным знаком:

(*) х -диф. уравн. 2-го порядка (условие гармоничности х)

Докажем, что только уравнения типа: х=х_max sinωt и х=х_max соsωt

удовлетворяют уравнению (*): 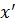=( 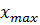sin ωt)^’=ωx_max соsωt.

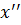=( ωx_max соsωt)^’= -ω²x_max sinωt= -ω²x.

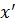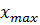=( cos ωt)^’=-ωx_max sinsωt.

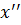=(- ωx_max sinωt)^’= -ω²x_max codωt= -ω²x. Следовательно:

Вывод: уравнения типа х= х=хmax sinωt sinωt и х=хmaxсоs ωt являются гармоническими.

Характеристики гармонических уравнений

х=хmax sinωt

х=х_max соsωt , х_max_–амплитуда колебания, ωt – фаза колебаний,

ω – циклическая частота колебаний.

СИ 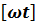-рад, СИ 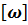-рад/с, СИ 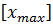- м (если речь о механических колеб)

Амплитудой гармонических колебаний х_max называется наибольшее значение колеблющейся величины, которое стоит перед знаком sin или соs в уравнении гармонических уравнений.

Периодомгармонических колебаний Т называется время одного колебания

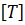Т = ; СИ - с

Частотой гармонических колебаний υ называется количество колебаний в единицу времени.

υ = 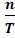; СИ 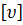- с^-1; Гц.

Фазой гармонических колебаний φ называется физическая величина, стоящая под знаком sin или соs в уравнении гармонических уравнений и которая при заданной амплитуде однозначно определяет значение колеблющейся величины.

φ=ωt ; СИ 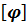-рад.

Докажем, что колебания маятников гармонические:

а) пружинный:F_упр = -kx = ma; ⇒ a = - x ; Т.к. a = x^”, то имеем:

x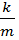^”= - x ⇒ пружинный маятник колеблется гармонически. Т.к. ω²= 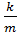⇒ ω = 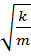= 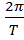; откуда Т = 2π 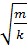- формула периода колебаний пружинного маятника.

б) математический (груз, подвешенный на невесомой и нерастяжимой нити, размерами которого по сравнению с ее длиной можно пренебречь)

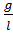F_равнод= -mgsinφ =ma; ⇒ -gsinφ =a =x^”; Т.к. sinφ= ⇒ - g = ^“x= -ω²x; ⇒ математический маятник колеблется гармонически. Т.к. ω²= ⇒ ω = = 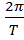; откуда Т = 2π 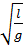- формула периода колебаний математического маятника.

Экспериментальное задание:экспериментально найти период колебаний пружинного маятника, его х_max , записать уравнение его колебаний и найти v_max и a_max .(пружина с жескостью 40 Н/м, груз 400г)

Т≈0,67 с ⇒ υ= = 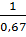≈1,5 Гц ⇒ х =0,05cos2π1,5t = 0,05cos3πt .

V= 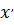(t)= - 0,15πsin3πt ; a= 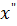(t)=-0,45π²cos3πt

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒