Тема занятия «Основные понятия комбинаторики: размещения, сочетания, перестановки»

Стр 1 из 3Следующая ⇒

15.06.2020

Тема занятия «Основные понятия комбинаторики: размещения, сочетания, перестановки»

План занятия

1. Посмотреть видеоуроки:

https://www.youtube.com/watch?v=KbtoJjtK1v4&list=PLHYZenZg0FRk6xGTEcDVaE-3KWX1V466I&index=53

https://www.youtube.com/watch?v=QOooeUhL4bo&list=PLHYZenZg0FRk6xGTEcDVaE-3KWX1V466I&index=55

https://www.youtube.com/watch?v=hINtwMR2dQs&list=PLHYZenZg0FRk6xGTEcDVaE-3KWX1V466I&index=57

2. Законспектировать теоретический материал:

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения.Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

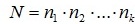
способами.

12 3 Следующая ⇒