(2)ó EABC(t,t1,t0)= eAB(t) + eBA(t0) (3)

(2)ó EABC(t, t1, t0)= eAB(t) + eBA(t0) (3)

- Xé ttạ ithờ iđ iể m t = t₀= const ta có:

- E_ABC(t, t₁, t₀)= 0 (do khô ngcó sự chê nhlệ chvề nhiệ tđ ộ giữ a 2 mố ihà n) nê nsứ cđ iệ nđ ộ ngtổ ngbằ ng 0 theođ ú ngnguyê nlý củ ahiệ uứ ngnhiệ tđ iệ n.

ð E_ABC(t, t₁, t₀) = e_AB(t₀) + e_BA(t₀) = 0

ó e_B_A(t₀)= -e_AB(t₀) (4)

Thế (4) và (3) ta đ ư ợ c phư ơ ng trì nh:

E_ABC(t, t₁, t₀)= e_AB(t) - e_AB(t₀) (Đ PCM)

Vậ yta có kế t luậ n: khi thê m và o dâ y dẫ n C tạ i nhiệ t đ ộ tiế p xú c t₁ thì sứ c đ iệ n đ ộ ng tổ ng củ a cặ p nhiệ t đ iệ n khô ng đ ổ i và bằ ng vớ i sứ c đ iệ n đ ộ ng trong phư ơ ng trì nh cơ bả n củ a cặ p nhiệ t đ iệ n:

EABC(t, t1, t0)= EAB(t, t0)=eAB(t)-eAB(t0)

Câ u 14: Hã ychứ ng minh phư ơ ngtrì nhcơ bả ncủ acặ pnhiệ tđ iệ ncó sứ cđ iệ nđ ộ ngtổ ngcộ ngcủ acặ pnhiệ tđ iệ nchỉ phụ thuộ cvà ohiệ ucủ asứ cđ iệ nđ ộ ngsinhratrê nhaidâ ydẫ n AB khixả yrachê nhlệ chnhiệ tđ ộ t và t0 tạ ihaimố ihà n:

EAB(t, t0)=eAB(t)-eAB(t0)?

Phư ơ ngtrì nhcơ bả ncủ acặ pnhiệ tđ iệ nlà: E_AB(t, t₀)=e_AB(t)-e_AB(t₀) (1)

Sơ đ ồ nguyê nlý củ acặ pnhiệ tđ iệ n

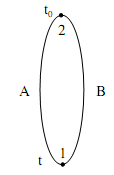
Phư ơ ng trì nh sứ c đ iệ n đ ộ ng tổ ng:

E_ABC(t, t₀)= e_AB(t) + e_BC(t₀) + e_CA(t₀) + e_A(t₀, t) + e_A(t, t₀) + e_B(t, t₀) + e_B(t₀, t) (2)

Ta có: Cặ p sứ c đ iệ n đ ộ ng sinh ra trê n từ ng dâ y dẫ n do chê nh lệ ch nhiệ t đ ộ giữ a hai đ ầ u dâ y A, B lầ n lư ợ t là:

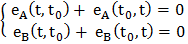
Do cá c cặ p sứ c đ iệ n đ ộ ng tạ o ra có cù ng đ ộ lớ n như ng ngư ợ c hư ớ ng nê n chú ng tự triệ t tiê u nhau.

(2)ó EAB(t, t0)= eAB(t)+ eBA(t0) (3)

- Xé ttạ ithờ iđ iể m t = t₀= const ta có:

- Ta có E_AB(t, t₀)= 0 (do khô ngcó sự chê nhlệ chvề nhiệ tđ ộ giữ a 2 mố ihà ntheonguyê nlý củ ahiệ uứ ngnhiệ tđ iệ n).

ð E_AB(t, t₀) = e_AB(t₀) + e_BA(t₀) = 0

ó e_BA(t₀) =- e_AB(t₀) (4)

Thế (4) và (3) ta đ ư ợ c phư ơ ng trì nh:

E_AB(t, t₀)= e_AB(t) - e_AB(t₀) (đ pcm)

⇐ Предыдущая 2 3 4 5 6 7 8910 11 Следующая ⇒