
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
09.11.21_Предел функции. Раскрытие неопределенностей
09. 11. 21_Предел функции
Вспомним:
Предел функции ( предельное значение функции ) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом 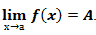 .
.
Вычислим предел: 
Подставляем вместо х – 3. 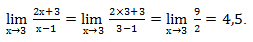
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы 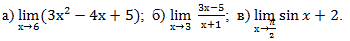
Опр: Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).
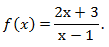
Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.
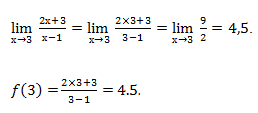
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
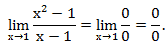
Основные виды неопределенностей: 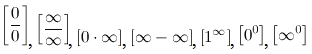
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
- упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т. д., и т. п.;
- если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: вычислим предел. 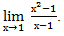
Разложим числитель на множители 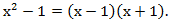
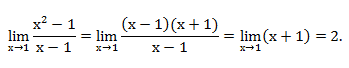
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|