Четырехугольники

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

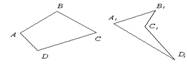Выпуклый ABCD и невыпуклый A₁B₁C₁D_1.

Две несмежные стороны, две вершины, не являющиеся соседними, четырехугольника называются противоположными.

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

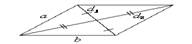Свойства параллелограмма: противоположные стороны равны; противоположные углы равны; диагонали точкой пересечения делятся пополам; сумма углов, прилежащих к одной стороне, равна 180°; биссектриса угла параллелограмма отсекает от него равнобедренный треугольник; сумма квадратов диагоналей равна сумме квадратов всех сторон: d₁²+d₂²=2(a²+b²).

Признаки параллелограмма. Четырехугольник является параллелограммом, если: 1) две его противоположные стороны равны и параллельны; 2) противоположные стороны попарно равны; 3) диагонали точкой пересечения делятся пополам. Площадь параллелограмма:

S = ah_a или S = ab sin α или S = 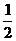d₁d₂ sin φ , где a и b — смежные стороны; α — угол между ними; h_a— высота, к стороне a. d₁, d₂ — диагонали; φ — угол между ними.

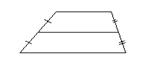Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.

Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Свойства трапеции: ее средняя линия параллельна основаниям и равна их полусумме ;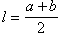

если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

если трапеция равнобокая, то около нее можно описать окружность;

если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

Признак трапеции: четырехугольник является трапецией, если его параллельные стороны не равны .

Площадь трапеции:

S= 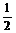(a+b)h или S = lh a и b — основания; h – высота; l — средняя линия.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника: диагонали равны. И все свойства параллелограмма.

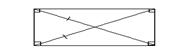Признаки прямоугольника. Параллелограмм является прямоугольником, если: 1) один из его углов прямой; 2) его диагонали равны . Площадь прямоугольника:

12 Следующая ⇒