Контакты

Случайная статья

Пример 28.2.. 28.3. Нахождение наибольших и наименьших значений функции. Пример 28.3.

⇐ ПредыдущаяСтр 2 из 2

Пример 28. 2.

Исследовать на экстремум функцию .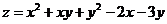

Решение.

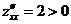, , - (минимум)

Найдем точки минимума.

По теореме 28. 2. 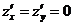, т. е. 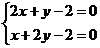, x=1/3, y=4/3

Итак, в точке 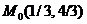функция имеет минимум.

28. 3. Нахождение наибольших и наименьших значений функции

Чтобы вычислить наибольшее и наименьшее значение функции 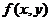в замкнутой области, поступают следующим образом:

1) находят все максимальные и минимальные значения функции, достигаемые в данной области;

2) находят наибольшие и наименьшие значения функции 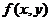на границе области.

3) сравнивают найденные значения.

Пример 28. 3.

Найти наибольшее значение функции 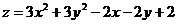в замкнутой области, ограниченной линиями: , , .

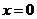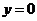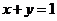Решение.

1) , 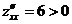(min) .

2) 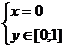, , 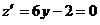=> y=1/3.

z(0)= 2, z(1/3)=1/3-2/3+2=4/3; z(1)=3.

при x=0, z=3(наибольшее).

3) 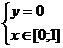, 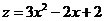аналогично при y=0, z=3 (наибольшее);

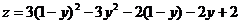
4) x+y=1; 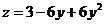12y-6=0 y=1/2

z(0)=3, z(1)=3, z(1/2)=3/2

Итак, наибольшее значение: 3 при y=0 или y=1.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.