Лекция 28. 28.1. Частные производные и дифференциалы высших порядков. Определение 28.1.. Пример 28.1.. Теорема 28.1.. Определение 28.2.. 28.2. Экстремумы функции двух переменных

Стр 1 из 2Следующая ⇒

Лекция 28

28. 1. Частные производные и дифференциалы высших порядков

Определение 28. 1.

Частные производные по переменным 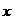и 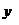в точке 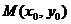от функци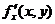й и 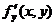в точке М, если они существуют, называются

частными производными второго порядка от функции .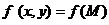

Обозначение.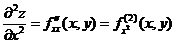

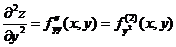
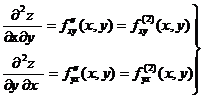– смешанные частные производные.

Пример 28. 1.

Найти частные производные функции .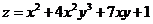

Решение.

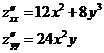
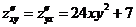Теорема 28. 1.

Если функци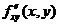и и 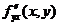существуют в 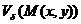и непрерывны в самой точке М, то они равны между собой:

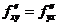(28. 1).

Определение 28. 2.

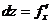
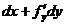– дифференциал первого порядка

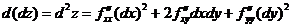– дифференциал второго порядка.

Тогда

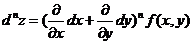– дифференциал n-го порядка

28. 2. Экстремумы функции двух переменных

Пусть функция 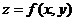определена в окрестности точки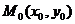

Определение 28. 3.

Функция 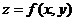имеет в точки 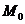локальный максимум (минимум), если существует 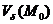: 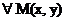из окрестности выполняется неравенство:

( )

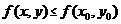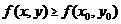Таким образом, в окрестности точки :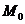

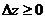
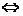локальный минимум,

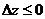
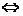локальный максимум.

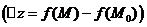
Теорема 28. 2 (необходимое условие экстремума).

Если функция 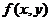имеет в точке 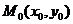экстремум и частные производные первого порядка, то выполняется равенство:

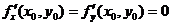(28. 2).

Точки, в которых выполняется равенство (28. 2) называются точками возможного экстремума, или стационарными точками.

Теорема 28. 3 (достаточное условие экстремума).

Пусть в точке 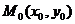возможного экстремума и некоторой ее окрестности функция 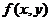имеет непрерывные частные производные второго порядка.

Положим

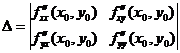
Тогда: а) если 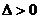, то в точке 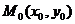экстремум: ;

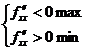б) если 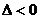, нет экстремума;

в) если 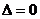, требуется дополнительное исследование.

12 Следующая ⇒