
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Правила дифференцирования суммы, разности, произведения и частного.
Правила дифференцирования суммы, разности, произведения и частного.
Если функции u=u(х) и v=v(x) дифференцируемы в точке х, то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)  0) также дифференцируемы в этой точке и имеют место следующие формулы:
0) также дифференцируемы в этой точке и имеют место следующие формулы:
1. dC=0, где С – константа.
2. d(u 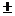 v)=du
v)=du 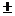 dv
dv
3. d(uv)=udv 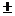 vdu
vdu
4. d(  )=
)= 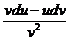
Доказать самостоятельно!
Инвариантность формы дифференциала.
Если y=f(u(x)) – сложная функция, то dy=f’(u)du, то есть форма дифференциала не меняется независимо от того, рассматривается y как функция независимой переменной x или зависимой переменной u.
Приближенные вычисления с помощью дифференциала. Из определения дифференциала следует, что он зависит линейно от 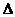 х и является главной частью приращения функции
х и является главной частью приращения функции 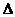 y.
y.
Если приращение 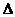 x аргумента x близко к нулю, то приращение
x аргумента x близко к нулю, то приращение 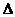 y функции приближенно равно ее дифференциалу, то есть
y функции приближенно равно ее дифференциалу, то есть 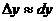 , откуда
, откуда 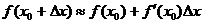 .
.
Последняя формула удобна для приближенного вычисления значения функции f(x) в точке 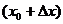 по известному значению этой функции в точке
по известному значению этой функции в точке  .
.
Во многих задачах приращение функции в данной точке приближенно заменяют дифференциалом функции в этой точке.
Дифференциалы высших порядков.
Рассмотрим функцию 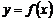 . Дифференциал этой функции
. Дифференциал этой функции 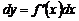 зависит от
зависит от 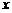 и
и 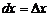 , причем
, причем 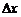 от
от 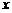 не зависит, так как приращение в данной точке
не зависит, так как приращение в данной точке 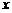 можно выбирать независимо от точки
можно выбирать независимо от точки 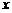 . Поэтому
. Поэтому 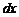 в формуле первого дифференциала будет постоянным. Тогда выражение
в формуле первого дифференциала будет постоянным. Тогда выражение 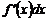 зависит только от
зависит только от 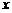 и его можно дифференцировать по
и его можно дифференцировать по 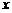 .
.
Дифференциал от дифференциала функции 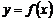 в данной точке
в данной точке 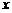 называется дифференциалом второго порядка или вторым дифференциалом и обозначается
называется дифференциалом второго порядка или вторым дифференциалом и обозначается 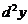 или
или 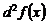 , т. е.
, т. е. 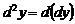 . Полагая
. Полагая 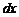 в формуле
в формуле 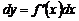 первого дифференциала постоянным, получим:
первого дифференциала постоянным, получим:
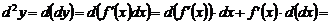
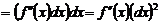 .
.
Аналогично определяется дифференциал третьего порядка 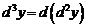 и он равен:.
и он равен:.
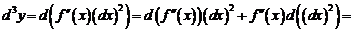
 .
.
Дифференциал 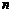 -го порядка (или
-го порядка (или 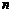 -й дифференциал) функции
-й дифференциал) функции 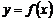 определяется как дифференциал от дифференциала
определяется как дифференциал от дифференциала 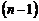 -го порядка:
-го порядка: 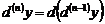 и
и 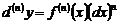 .
.
Скобки при степенях 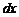 можно опустить:
можно опустить: 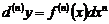 .
.
Отсюда следует, что производная 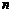 -го порядка функции
-го порядка функции 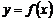 есть отношение ее дифференциала
есть отношение ее дифференциала 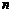 -го порядка к
-го порядка к 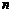 -й степени дифференциала независимой переменной:
-й степени дифференциала независимой переменной:
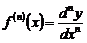 .
.
В частности, при  получим соответственно:
получим соответственно:
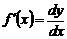 ,
, 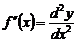 ,
, 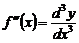 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|