Дифференциал функции имеет геометрический смысл.

Лекция 14. Понятие дифференциала функции.

Определение. Функция f(x)называется дифференцируемой в точке х₀, если ее приращение 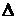у в этой точке можно представить в виде

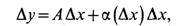
где А — некоторое число, не зависящее от 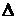х, а 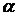( 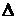х) - функция аргумента 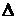х, являющаяся бесконечно малой при 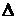х 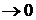, т. е. .

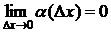Выясним связь между дифференцируемостью в точке и существованием производной в той же точке.

Теорема 14. 1. Для того чтобы функция f(x) была дифференцируема в данной точке х₀ необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Таким образом, для функций одной переменной дифференцируемость и существование производной - понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.

Связь между понятиями дифференцируемости и непрерывности описывается следующей теоремой.

Теорема 14. 2. Если функция y=f(x) дифференцируема в данной точке
х₀, то она и непрерывна в этой точке.

Замечание. Обратное утверждение не верно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т. е. не иметь производной в этой точке.

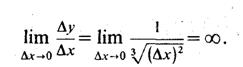
Это значит, что функция f(x) = 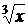в точке х=0 не имеет конечной производной, т. е. не является дифференцируемой.

Пусть функция f(x) дифференцируема в точке х₀, т. е. приращение 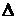у можно записать в виде суммы двух слагаемых:

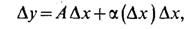
где .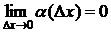

Определение. Дифференциалом функции f(х) в точке х₀ называется главная, линейная относительно 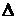х часть приращения функции:

dy=A 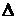x (14. 1)

По теореме 14. 1 учтя, что А = 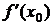, то формулу (14. 1) можно записать в виле dy=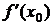 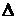х. (14. 2)

Дифференциалом независимой переменной х назовем приращение этой переменной: dx= 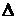x. Тогда

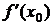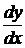= (14. 3)

Дифференциал функции имеет геометрический смысл.

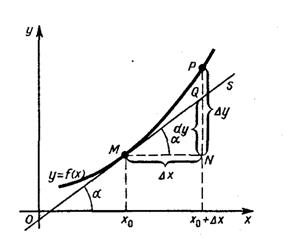
Пусть точка М на графике функции y=f(x) соответствует значению аргумента , точка Р—значению аргумента 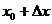, прямая MS—касательная к графику y=f(x) в точке М, 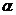- угол между касательной и осью Ох. Пусть, далее, MN\\Ox, PN\\Oy, Q—точка пересечения касательной MS с прямой PN. Тогда приращение функции 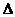у равно величине отрезка NP. В то же время из прямоугольного треугольника MNQ получаем NQ=tg 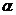=f'( ) 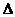x=dy, т. е. дифференциал функции dy равен величине отрезка NQ. Из геометрического рассмотрения видно, что величины отрезков NP и NQ различны.

Таким образом, дифференциал dy функции y=f(x) в точке равен приращению «ординаты касательной» MS к графику этой функции в точке М( 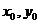), а приращение функции 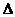у есть приращение «ординаты самой функции» y=f(x) в точке , соответствующее приращению аргумента, равному 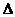x.

12 Следующая ⇒