
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Tabulka 1: Porovnání teoretických a naměřených hodnot.
3. 3 Dá l jsme experimentá lně na vlastní noze odhadli prů ř ez naš ich quadricepsu a teoreticky stanovili maximá lní mož nou sí lu, kterou mohou vytvoř it.
Praví tka jsem změ ř ila hodnotu odejmutí své nohy a z ně j, pomoci vzorku pro geometrický obvod a plochu, vypoč í tala jsem hodnotu prů ř ezu:
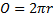
Kde 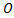 je geometricky obvod,
je geometricky obvod, 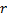 je polomer stehna.
je polomer stehna.
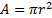
Kde 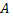 je plocha.
je plocha.
Ze vzorku (4) plyne:
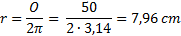
Hodnotu prů ř ezu zí ská me pomoci vzorce (5):
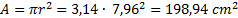
Z pokynu k zpracová ní ú lohy ví me, ž e 1 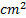 svalové tká ně mů ž e generovat př ibliž ně 50N.
svalové tká ně mů ž e generovat př ibliž ně 50N.
Ná sobení m té to hodnoty hodnotou prů ř ezu stehna maximá lní mož nou sí lu, kterou teoreticky mů ž e vytvoř it:
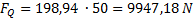
3. 4 Zatí m jsme stanovili potř ebnou sí lu svalů k zachová ní statické polohy v podř epu.
Potř ebovali jsme pro to vedet hmotnost horní č á sti trupu, již č iní dvě tř etiny hmotnosti celé ho trupu. Totiž, když já mam vá hu 55 kg, př i vypoč tu dostanu ná sledují cí hodnotu:
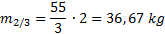
Dosazení m do vzorce (3) zí skala jsem tí hovou silu tě la:
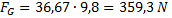
Ná sledně, pomoci vzorce (2), dostala jsem hledanou hodnotu sí ly svalů v podř epu:
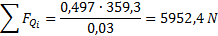
3. 5 Nakonec jsme musili stanovit minimá lní rozmě ry menisků v koleni, aby nedoš lo k př edč asné artró ze. Za př edpokladu zjednoduš ení jsme znovu použ ili sché ma silový ch pomě rů na tibiofemorá lní č á sti s uvá ž ení m extenzorů kolene. V tomto př í padě platí podmí nka momentové rovnová hy:
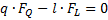
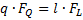
Potř ebovali jsme také vedet vý slednice dvou sil, pů sobí cí ch na patelu: silu M. quadricepsu a vazu lig. Patellae. Vypoč í tali jsme ji pomocí kosinové vě ty:
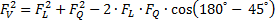
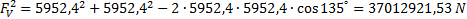
Podle tř etí ho Newtonova zá kona a silové podmí nky rovnová hy platí, ž e vý sledná sila se po modulu rovna sily pů sobí cí na menisky a má opač ný smě r:
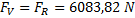
Zná me li, ze maximá lní mož né zatí ž eni č iní 20 MPa, mů ž eme vypoč í tat rozmě ry menisku odvození m ze vzorce tohoto parametru:
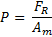
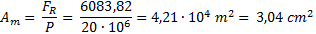
Tí m způ sobem jeden meniskus má velikost dva krá t menš í:
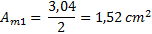
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|