ЛАБОРАТОРНАЯ РАБОТА № 4. Составить математическую модель для следующей задачи.. Решить задачу графическим методом.. Решение с помощью MS Excel.

ЛАБОРАТОРНАЯ РАБОТА № 4

Составить математическую модель для следующей задачи.

Решить задачу графическим методом.

Из трех сортов бензина образуются две смеси. Первая состоит из А₁ 60% бензина первого сорта, В₁ 20% бензина 2-го сорта, С₁ 20% бензина 3-го сорта; вторая – А₂ 30% - 1-го, В₂ 20% - 2-го, С₂ 50% - 3-го сорта. Цена 1-ой смеси - Z₁ 305 у. е., второй - Z₂ 200 у. е. за тонну. Сколько смеси первого и второго вида можно изготовить из “а” 24тонн 1-го сорта, “в” 10 тонн 2-го сорта и “с” 16 тонн 3-го сорта, чтобы получить максимальный доход?

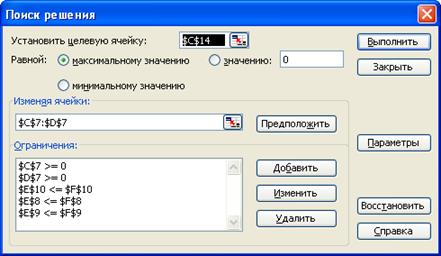
Максимальный доход определить с помощью надстройки Поиск решения.

Решение:

Обозначения: х1 – колич-во смеси 1-го вида

х2 – колич-во смеси 2-го вида

Тогда доход: f(x) = 305*x1 + 200*x2 – max;

Расход бензина на изготовление х1 смеси 1-го вида:

1-го сорта: 0, 6*х1

2-го сорта: 0, 2*х1

3-го сорта: 0, 2*х1

Расход бензина на изготовление х2 смеси 2-го вида:

1-го сорта: 0, 3*х2

2-го сорта: 0, 2*х2

3-го сорта: 0, 5*х2

Следовательно, можно подсчитать расход бензина каждого сорта при планируемом выпуске смеси: х1, х2:

Расход 1-го сорта: 0, 6*х1 + 0, 3*х2

Расход 2-го сорта: 0, 2*х1 + 0, 2*х2

Расход 3-го сорта: 0, 2*х1 + 0, 5*х2

Так как количество бензина каждого сорта ограничено, это нужно учесть ограничениями (неравенствами).

0, 6*х1 + 0, 3*х2 < = 24

0, 2*х1 + 0, 2*х2 < = 10

0, 2*х1 + 0, 5*х2 < = 16

Следовательно, математическая модель этой задачи следующая:

найти

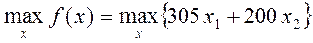
при ограничениях:

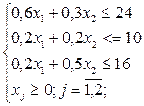Решение с помощью MS Excel.

Введем в таблицу исходные данные и расчетные формулы.

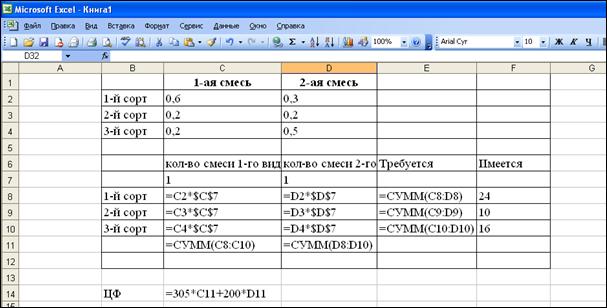
Используя надстройку Поиск решения найдем максимальный доход.

12 Следующая ⇒