
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
а) длину вектора , если точка А(3;-1;5) и В(2;3;-4)
⇐ ПредыдущаяСтр 2 из 2
а) длину вектора , если точка А(3; -1; 5) и В(2; 3; -4)
б) скалярное произведение векторов 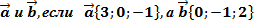
Решение:
а) 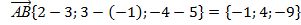
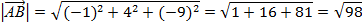
б) 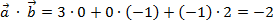
Ответ:
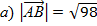 б)
б) 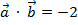
3. Найдите угол между векторами 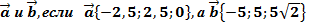
Решение:
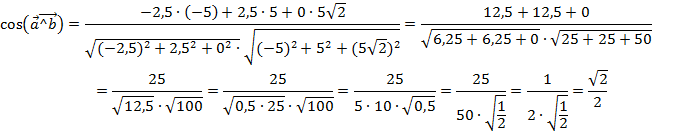
Отсюда следует, что угол между векторами 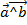
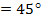
Ответ: 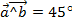
4. Даны точки М(2; -1; 3), N(-4; 1; -1), P(-3; 1; 2) и Q(1; 1; 0). Вычислить расстояние между серединами отрезков MN и PQ (на рис. АВ)
Решение:
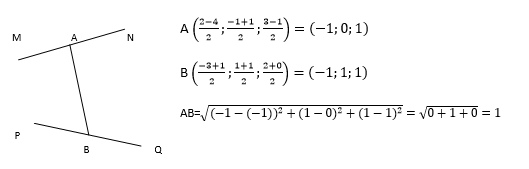
5. Определить вид ∆ АВС, если А(2; 4; -1), В(4; 8; -2) и С(0; 0; 0)
Решение:
Найдем длины сторон треугольника АВ, ВС и АС
АВ= 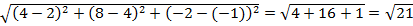
ВС= 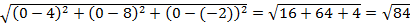
АС= 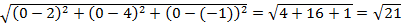
АВ=АС => ∆ АВС равнобедренный
Ответ: ∆ АВС равнобедренный
Содержание работы
| I вариант | II вариант |
1. Найдите координаты вектора  , если , если 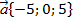 , , 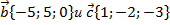 , a , a 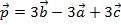
| 1. Найдите координаты вектора  , если , если 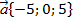 , , 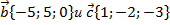 , a , a 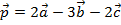
|
2. Найдите:
a) длину 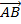 , если А(-1; 0; 2) и В(1; -2; 3)
б) скалярное произведение векторов , если А(-1; 0; 2) и В(1; -2; 3)
б) скалярное произведение векторов 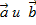 , если , если 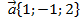 и и 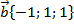
| 2. Найдите:
a) длину 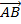 , если
А(-35; -17; 20) и В(-34; -5; 8)
б) скалярное произведение векторов , если
А(-35; -17; 20) и В(-34; -5; 8)
б) скалярное произведение векторов 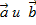 , если , если 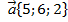 и и 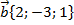
|
3. Найдите угол между векторами:
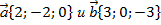
| 3. Найдите угол между векторами:
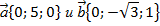
|
| 4. Даны точки А(3; 5; 4), B(4; 6; 5), C(6; -2; 1) и D(5; -3; 0). Найдите расстояния между серединами отрезков AB и CD. | 4. Даны точки А(3; 5; 4), B(4; 6; 5), C(6; -2; 1) и D(5; -3; 0). Найдите расстояния между серединами отрезков AC и BD. |
| 5. Определить вид треугольника ABC, если: A(9; 3; -5), B(2; 10; -5) и C(2; 3; 2) | 5. Определить вид треугольника ABC, если: A(3; 7; -4), B(5; -3; 2) и C(1; 3; -10) |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|