ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 23. Образец выполнения заданий.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 23

Тема: Координатный метод решения задач

Цель закрепить знания и совершенствовать умения по нахождению координат точек и координат векторов, нахождение скалярного произведения векторов, а также выполнять простейшие задачи в координатах.

Краткие теоретические сведения
Действия с векторами в координатной форме:

Правило 1. Суммой (разностью) векторов 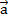(х₁; у₁; z₁) и 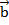(х₂; у₂; z₂) называется вектор = 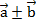, координаты которого равны сумме (разности) соответствующих координат этих векторов:

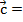(х₁ 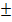х₂; у₁ 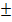у₂; z₁ 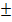z₂).

Правило 2. Произведением вектора 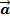(х; у; z) на число k называется вектор

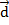=k 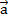, координаты которого равны произведению числа k на координаты вектора :

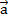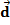=(kх; kу; kz).

Правило 3. Для определения координат вектора АВ нужно от координат конца вектора вычесть координаты начала.

Координаты вектора 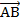выражаются через координаты его начала А(х ₁; у ₁; z ₁ ) и конца В(х ₂; у ₂; z ₂ ):

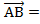{ х₂ – х₁, у₂ – у₁, z₂ – z₁}.

Длина вектора 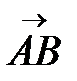вычисляется по формуле:

.

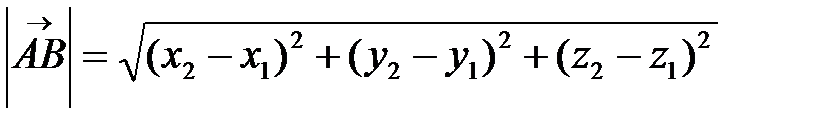Скалярное произведение векторов 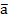= {a_x; a_y; a_z} и 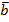= {b_x; b_y; b_z} можно найти воспользовавшись следующей формулой:

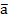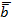· = a_x · b_x + a_y · b_y + a_z · b_z

Формула вычисления угла между векторами:

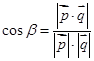
Образец выполнения заданий.

1. Найдите координаты вектора 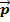, если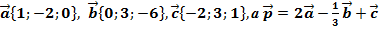

Решение:

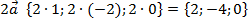
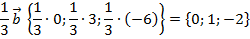
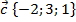
Получаем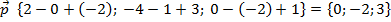

Ответ: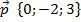

2. Найдите:

12 Следующая ⇒