4 Комплексное изображение синусоидальных функций времени

4 Комплексное изображение синусоидальных функций времени

Данный метод совмещает простоту и наглядность векторных диаграмм с возможностью проведения точных аналитических расчетов.

Перенесем радиус-вектор, изображающий синусоидальную функцию времени (см. рисунок 1) в декартовой плоскости, на комплексную плоскость. При этом совместим ось х с осью действительных чисел (+1, Re), а ось у - с осью мнимых чисел (+j, Im) – рисунок 2.

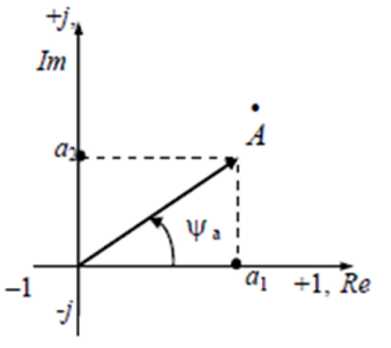
Рисунок 2

Тогда любому вектору Ā, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:

1) алгебраическая форма записи

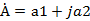
2) тригонометрическая форма записи

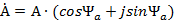
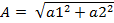– модуль комплексного числа (амплитуда)

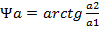- аргумент комплексного числа (начальная фаза)

3) показательная форма записи

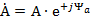
е - основание натурального логарифма.

⇐ Предыдущая 12