Вопрос 2 СПОСОБЫ ПРЕДСТАВЛЕНИЯ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН

ТЕМА 4 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Вопрос 2 СПОСОБЫ ПРЕДСТАВЛЕНИЯ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН

1 В виде тригонометрических функций

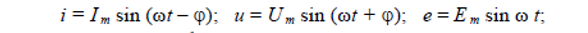
2 В виде временных диаграмм

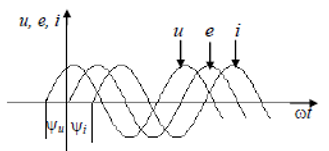
3 В виде вращающихся векторов

Вектор Аr вращается в декартовой плоскости против часовой стрелки. В соответствии с определением синуса проекция вращающегося радиуса-вектора на ось у равна

в момент времени t = 0: a = a0 = Am*sin Ψ a

в момент времени t1: a1 = Am*sin (ω *t1+ Ψ a)

Здесь Ψ a - начальная фаза. Ψ 1 = Ψ a + ω *t1; Ψ 2 = Ψ a + ω *t2.

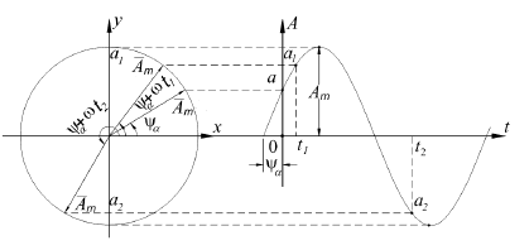
Рисунок 1

На рисунке справа построена синусоида, мгновенные значения которой для любого момента времени t найдены как соответствующие проекции вращающегося радиуса-вектора на ось у. На основании этих построений можно утверждать, что любая синусоидальная функция может быть изображена (условно) однозначно соответствующим ей вращающимся радиусом-вектором, длина которого равна амплитудному значению синусоиды, а начальное положение относительно оси x определяется начальной фазой синусоиды.

Совокупность радиусов-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой. Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты. Суммирование и вычитание векторов гораздо проще, чем тригонометрических функций, поэтому метод очень распространён - он прост и нагляден.

12 Следующая ⇒