Косинус разности: cos (α-β)=cos α·cos β+sin α·sin β (4)

Косинус разности: cos (α -β )=cos α ·cos β +sin α ·sin β (4)

Тангенс суммы: (5)

Тангенс разности: (6)

Котангенс суммы: 𝒄 𝒕 𝒈 a+𝜷 =𝒄 𝒕 𝒈 a •𝒄 𝒕 𝒈 𝜷 − 𝟏 𝒄 𝒕 𝒈 a+𝒄 𝒕 𝒈 𝜷 (7)

Котангенс разности: (8)

Примеры сложения и вычитания с помощью тригонометрических формул.

Пример 1

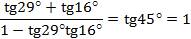(по формуле 5)

Ответ: 1

Пример 2. Найти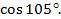

Представим 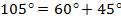, так как нам известны значения косинуса углов 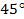и 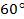Подставим в формулу косинуса суммы. Получаем:

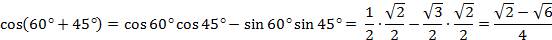Ответ: .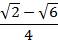

Пример3. Вычислите .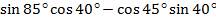

Применяем формулу синуса разности: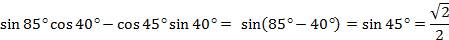

Ответ: .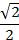

2. Формулы синуса, косинуса, тангенса и котангенса двойного аргумента.

Воспользуемся формулами косинуса и синуса суммы аргументов

Sin(α +β )=Sinα Cosβ +Sinβ Cosα

Cos(α +β )=Cosα Cosβ – Sinα Sinβ

Могут ли в данных формулах углы быть равными? (Да)

Как тогда будут выглядеть левая часть выражения, подставить в формулу вместо β

значение α?

Sin(α +α ) = Sin2α

Cos(α +α ) = Cos2α

Как можно назвать полученные выражения? (Синус двойного угла и косинус двойного угла)

Это и есть тема нашего урока. Данные формулы справедливы для любых значений углов. Формулы работают как слева направо, так и справа налево.

Выведим формулы двойного угла, используя формулы суммы. Продолжим начатые записи, применяя формулы суммы.

Sin(α +α ) = Sin2α = Sinα Cosα + Sinα Cosα = 2 Sinα Cosα

Cos(α +α ) = Cos2α =Cosα Cosα – Sinα Sinα = Cos2α – Sin2α

Запишите в тетрадь полученные результаты: