
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение. Теорема
Определение
Медианой называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Теорема
Три медианы треугольника пересекаются в одной точке и делятся ей в отношении 2: 1, считая от вершины.
Дано: треугольник 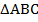 ,
, 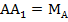 – медиана к стороне ВС,
– медиана к стороне ВС, 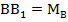 – медиана к стороне АС,
– медиана к стороне АС, 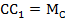 – медиана к стороне АВ, точка М – точка пересечения медиан.
– медиана к стороне АВ, точка М – точка пересечения медиан.
Доказать: точка М – точка пересечения есть и единственная; 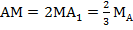 ,
, 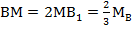 ,
, 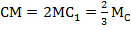 .
.
Доказательство:
Соединим точки В1 и С1. С1В1 – средняя линия треугольника 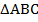 (см. Рис. 2). Отсюда треугольник
(см. Рис. 2). Отсюда треугольник 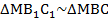 . Они подобны по равенству двух углов (углы
. Они подобны по равенству двух углов (углы 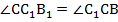 как внутренние накрест лежащие при параллельных прямых ВС и В1С1 и секущей СС1, углы
как внутренние накрест лежащие при параллельных прямых ВС и В1С1 и секущей СС1, углы 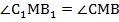 как вертикальные). Мы знаем, что средняя линия равна половине основания треугольника, то есть
как вертикальные). Мы знаем, что средняя линия равна половине основания треугольника, то есть 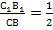 , отсюда коэффициент подобия данных треугольников
, отсюда коэффициент подобия данных треугольников 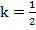 . Все линейные элементы треугольников соотносятся с
. Все линейные элементы треугольников соотносятся с
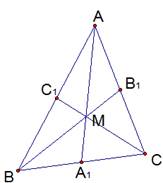
Рис. 2
таким коэффициентом подобия, отсюда 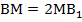 и
и 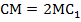 . Аналогично из подобия треугольников
. Аналогично из подобия треугольников 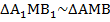 можно доказать, что
можно доказать, что 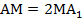 и
и 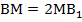 . Таким образом, если взять две медианы ВВ1 и СС1, мы докажем, что медиана СС1 рассекает медиану ВВ1 в отношении 2: 1, аналогично медиана АА1 рассекает медиану ВВ1 в отношении 2: 1, а значит, все три медианы пересекаются в точке М, такая точка единственная, и она делит каждую медиану в отношении 2: 1, считая от вершины.
. Таким образом, если взять две медианы ВВ1 и СС1, мы докажем, что медиана СС1 рассекает медиану ВВ1 в отношении 2: 1, аналогично медиана АА1 рассекает медиану ВВ1 в отношении 2: 1, а значит, все три медианы пересекаются в точке М, такая точка единственная, и она делит каждую медиану в отношении 2: 1, считая от вершины.
3. Теоремы о прямоугольном треугольнике
Высота в прямоугольном треугольнике, проведенная из прямого угла, отсекает в нем два подобных треугольника, таким образом, получаем вместе с исходным три подобных треугольника.
Задан прямоугольный треугольник, угол 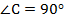 , высота СН (см. Рис. 3). Отрезок АН обозначается как
, высота СН (см. Рис. 3). Отрезок АН обозначается как 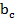 – это проекция катета b на гипотенузу с. Аналогично НВ это
– это проекция катета b на гипотенузу с. Аналогично НВ это 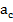 – проекция катета а на гипотенузу с. Гипотенуза СН обозначается
– проекция катета а на гипотенузу с. Гипотенуза СН обозначается 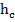 .
.
Основное свойство углов прямоугольника – их сумма составляет 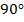 :
: 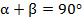 .
.
Если 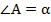 , то
, то 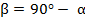
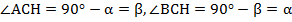 .
.
Таким образом, треугольники подобны по трем равным углам:
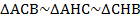
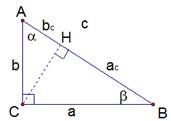
Рис. 3
Несложно заметить, что катет есть среднее геометрическое или среднее пропорциональное между гипотенузой и своей проекцией на нее:
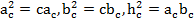
Данные равенства являются следствием доказанной теоремы о подобных треугольниках, отсеченных высотой. Докажем одну из них.
Теорема
Катет есть среднее геометрическое или среднее пропорциональное между гипотенузой и своей проекцией на нее.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|