Урок: Применение подобия к доказательству теорем и решению задач

Стр 1 из 2Следующая ⇒

Урок: Применение подобия к доказательству теорем и решению задач

1. Теорема о средней линии треугольника

Докажем с помощью подобия первую теорему.

Определение

Отрезок, соединяющий середины сторон треугольника, называют средней линией.

Свойства средней линии треугольника:

- средняя линия параллельна основанию треугольника;

- длина средней линии равна половине длины основания треугольника.

Теорема

Средняя линия треугольника параллельна основанию и равна его половине.

Дано: треугольник 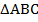. Точки M и N – середины сторон АВ и АС соответственно. Отрезок MN – средняя линия треугольника.

Доказать: , .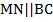

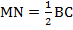Доказательство:

Рассмотрим треугольник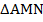и и 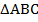(см. Рис. 1). Они подобны по углу и прилежащим к нему сторонам. Треугольники имеют общий угол и отношения сторон равны: .

То есть коэффициент подобия данных треугольников 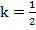и отношение всех линейных элементов равно 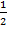. Таким образом, 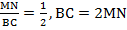, средняя линия треугольника равна половине основания.

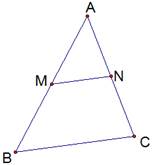
Рис. 1

Чтобы доказать параллельность средней линии и основания, нужно найти признаки параллельных прямых, для этого надо рассмотреть две прямые и секущую и найти равные углы. Поскольку треугольник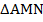и и 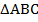подобны, все их соответствующие углы равны, таким образом 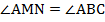, а это соответственные углы при пересечении двух прямых третьей, отсюда прямые MN и ВС параллельны, средняя линия треугольника параллельна его основанию.

2. Теорема о медианах треугольника

Докажем с помощью подобия свойство медиан треугольника.

12 Следующая ⇒