S есть (не есть) Р

В суждении «Донецк – областной центр Украины» субъектом (S) является понятие «Донецк», предикатом (Р) — понятие «областной центр Украины», связкой (в предложении ей соответствует тире) - глагол «есть».

В структуре простого суждения могут встречаться вспомогательные слова «некоторый», «все», «любой», «каждый», «ни один», «среди» и т. п. Эти слова называют кванторными словами. Они характеризуют суждение с его количественной стороны. Учитывая наличие в суждении кванторных слов, структуру простого суждения можно представить в виде следующих выражений: «Все S есть Р», «Ни одно S не есть Р», «Некоторые S есть/не есть Р».

По данным структурным элементам простых суждений проводится и их классификация.

По характеру предиката простые суждения делятся на атрибутивные, релятивные и экзистенциальные.

В атрибутивных суждениях предикат указывает на наличие или отсутствие у предмета некоторого свойства. К атрибутивным суждениям относятся, например, суждения «Донецк – областной центр Украины» и «Ни один человек не является бессмертным».

В релятивных суждениях (суждениях с отношениями) предикат указывает на тип отношения между предметами. Примерами релятивных суждений могут служить следующие суждения «Ромео и Джульетта любили друг друга», «Киев старше Москвы» и т. п.

В экзистенциальных суждениях (суждениях существования) предикат устанавливает существование или не существование некоторого предмета. Например: «Бог есть» или «Жизнь на Марсе не существует».

Впрочем, в традиционной логике релятивные и экзистенциальные суждения преобразуются в атрибутивные или категорические.

Простые категорические суждения являются наиболее простыми и удобными для логического анализа. В случае необходимости логического анализа суждений иного вида, их по возможности преобразуют в удобную для этого форму категорического суждения, представляя его в четкой логической форме.

В зависимости от количественной и качественной характеристики простых категорических суждений их принято делить на виды. Количественная характеристика суждения определяется тем, в каком объеме рассматривается в нем его субъект. Качественная характеристика суждения определяется характером его связки.

По своему качеству категорические суждения могут быть утвердительными или отрицательными. По количеству категорические суждения делятся на единичные, частные и общие.

Единичное суждение — это суждение, субъектом которого является единичное понятие. Примером такого рода суждения может быть следующее: «Автор поэмы «Гайдамаки» — Т. Г. Шевченко». Структуру единичного суждения можно представить как: «Данное S есть (не есть) Р».

Общее суждение — это суждение, в котором субъект взят в полном объеме. Например: «Всякая девушка красива» или «Ни один лгун не является честным человеком». Структура общего суждения имеет вид «Все S есть (не есть) Р».

Частное суждение - это суждение, в котором субъект взят в части своего объема. Например: «Некоторые люди являются любителями пива» или «Некоторые студенты нашего курса не употребляют спиртного».

Разновидностью деления суждений по количеству являются суждения (общие и частные) исключающие и выделяющие.

Исключающие суждения являются частными по смыслу и общими по форме. Например: " Все планеты, за исключением Венеры и Меркурия, имеют орбиты больше земной".

Выделяющие суждения отличаются особо определенным характером отношений между субъектом или предикатом: признак, выраженный предикатом, принадлежит только данному предмету, или предмету мысли присущ только данный предикат и никакой другой. Выделяющее суждение позволяет выразить мысль настолько определенно, что устраняет всякое иное ее толкование. Например: " Только должностное лицо может быть субъектом халатности" (суждение с выделяющим субъектом — только S есть Р)" Уголовное наказание применяется только по приговору суда" (суждение с выделяющим предикатом — S есть только Р).

Утвердительное суждение — это суждение, в котором указывается на принадлежность предиката этого суждения его субъекту. Иначе говоря, это суждение с утвердительной связкой «есть». Структура такого суждения (без учета количественной характеристики) имеет вид «S есть Р».

Отрицательное суждение — это суждение, в котором указывается на то, что предикат суждения не принадлежит его субъекту. Другими словами, это суждение с отрицательной связкой «не есть». Его структура (также без учета количественной характеристики): «S не есть Р».

Примеры: «Понятие (S) есть одна из форм мышления (Р)» - утвердительное суждение, «Некоторые предложения (S) не являются суждениями (Р)» — отрицательное суждение.

В традиционной логике (силлогистике) не делается различий между единичными и общими высказываниями, поскольку в них субъект берется в полном объеме.

Объединенная классификация категорических высказываний по качеству и количеству содержит четыре типа суждений: общеутвердительные (А), общеотрицательные (Е), частно-утвердительные (I) и частноотрицательные (О). Буквы А, Е, I, О для символических обозначений взяты из слова (лат. ) affirmo — утверждаю — для двух утвердительных высказываний и из слова (лат. ) nego — отрицаю — для двух отрицательных.

Этой классификацией мы будем пользоваться и в дальнейшем.

4. 2. РАСПРЕДЕЛЕННОСТЬ ТЕРМИНОВ В СУЖДЕНИЯХ.

Простые категорические суждения имеют характеристику, которая оказывается необходимой при анализе некоторых типов умозаключений. Эта характеристика называется распределенностью терминов. Распределенность того или иного термина в суждении связана с отношением терминов между собой.

Термин называется распределенным, если он рассматривается в этом суждении в полном объеме. Иначе говоря, термин распределен, когда он полностью включается в объем другого термина или полностью исключается из него.

В истинном общеутвердительном суждении ( А ), субъект всегда распределен, а предикат может быть распределен или нераспределен.

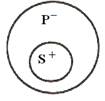
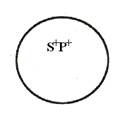
Например, в общеутвердительном суждении «Все кошки являются млекопитающими» субъект («кошки») распределен, а предикат (млекопитающие) не распределен. А в общеутвердительном суждении «Все квадраты – равносторонние прямоугольники» и субъект и предикат распределены, поскольку их объемы тождественны друг другу.

В истинном частноутвердительном суждении (I) в общем случае субъект не распределен, то же самое можно сказать и о предикате этого суждения.

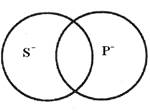
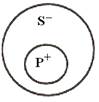
Схема общеотрицательного суждения (Е) ясно показывает, что в этом суждении оба термина распределены.

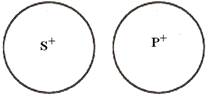
В частноотрицательном суждении (О) субъект так же не распределен, а предикат во всех представленных случаях оказывается распределенным.

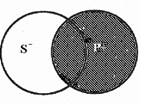
Итог этого анализа можно представить следующей таблицей (знак «+» означает, что термин распределен, а знак «-», что термин нераспределен):

A	S⁺	P ^-	S⁺	P⁺
E	S⁺	P⁺	-	-
I	S^-	P ^-	S^-	P⁺
O	S^-	P⁺	-	-

Между известными видами простых категорических суждений устанавливаются следующие отношения: противоречия (контрадикторности), противоположности (контрарности, противности), подпротивоположности (субконтрарности, подпротивности, или частичного совпадения) и подчинения.

Отношение противоречия (контрадикторности) устанавливается между суждениями, разными как по качеству, так и по количеству, т. е. между общеутвердительным (А) и частноотрицательным (О) и между общеотрицательным (Е) и частноутвердительным (I).

Отношение противоположности (контрарности, противности) устанавливается между общими суждениями, но разными по качеству: между общеутвердителным (А) и общеотрицательным (Е).

Отношение подпротивоположности (подпротивности, субконтрарности, или частичного совпадения) устанавливается между разными по качеству частными суждениями, (между I и О).

Наконец, в отношении подчинения находятся суждения одинакового качества, но разного количества, т. е. суждения общеутвердительное (А) и частноутвердительное (I), а также общеотрицательное (Е) и частноотрицательное (О). В этом отношении общее есть подчиняющее суждение, частное - подчиненное.

Для наглядности и лучшего запоминания отношений между простыми категорическими суждениями в качестве мнемонической фигуры используют предложенный еще в средневековье так называемый логический квадрат. Углы этого квадрата соответствуют видам суждений, а стороны и диагонали - отношениям между ними:

Рассмотрим теперь самое главное - истинностные зависимости суждений, находящихся в этих отношениях. Отношение противоречия (контрадикторности) - самое четкое и определенное, можно сказать, жесткое отношение между суждениями. Противоречащие суждения не могут быть одновременно ни истинными, ни ложными. Это отношение соответствует принципу логики, выраженному законом исключенного третьего, согласно которому, если суждение А (общеутвердительное) истинно, то противоречащее ему суждение О (частноотрицательное) будет обязательно ложным, и наоборот. Таково же отношение и между частноутвердительным (I) суждением и общеотрицательным (Е). Отношение противоположности (противности, контрарности) неоднозначно. При истинности суждения А (или Е} ему противное суждение Е (или А) будет обязательно ложным. Но при исходной ложности суждения А (или Е), ему противное суждение Е (или А) может быть как истинным, так и ложным, что зависит только от конкретного содержания этих суждений. И снова, в конкретной ситуации лишь специалист в этой предметной области может окончательно решить, каким именно по истинностному своему значению будет противоположное исходному суждение Например, исходное общеутвердительное (А) суждение «Все люди есть студенты» — ложно. По логике, противное ему суждение может быть как истинным, так и ложным. Зная предметную область, мы эту неопределенность снимаем и заключаем, что противное исходному общеотрицательное суждение (Е) «Ни один человек не является студентом» тоже ложно. Но вот другое по конкретному содержанию исходное суждение «Все люди имеют крылья». Оно тоже ложно, однако противное ему суждение «Ни один человек не имеет крыльев» — истинно. Особенность противоположных суждений кратко формулируется следующим образом: противоположные суждения не могут быть одновременно истинными, по крайней мере одно из них ложно, по большей мере - оба могут быть ложными. Отношение подпротивоположности (субконтрарности, частичного совпадения), можно сказать, обратно отношению противоположности, обратно по истинностным зависимостям. Это отношение устанавливается между разнокачественными частными суждениями, истинностные зависимости которых определяются нормой: подпротивоположные суждения не могут быть одновременно ложными, по крайней мере одно из них истинно, а по большей мере оба могут быть истинными. Так, при ложности исходного частноутвердительного суждения (I) ему подпротивное частноотрицательное суждение (О) будет обязательно истинным. То же самое и при ложности исходного частноотрицательного суждения — подпротивное ему суждение будет обязательно истинным. Например, суждение «Некоторые студенты имеют крылья» — ложно. Значит, подпротивное ему суждение должно быть обязательно истинным. И это так — «Некоторые студенты не имеют крыльев». Зато при истинности исходного частного суждения (I или О) ему подпротивное (О или I) может быть и истинным: " Некоторые студенты - спортсмены" и подпротивное ему " Некоторые студенты не есть спортсмены" оба истинны. Отношение подчинения характерно тем, что истинность общего (подчиняющего) суждения А (или Е) всегда влечет за собой истинность подчиненного ему частного суждения I (или О). Ложность же общих суждений не гарантирует ни истинности, ни ложности соответствующих им частных суждений, т. е. те могут быть в зависимости от конкретного содержания как истинными, так и ложными. Например, при истинности общего суждения «Все студенты - учащиеся», подчиняющееся ему частное суждение «Некоторые студенты - учащиеся» будет обязательно истинным. Ложность конкретного по содержанию общего суждения «Все студенты - отличники» позволяет конкретизировать истинностное значение подчиняющегося ему частного суждения «Некоторые студенты - отличники» — оно в данном случае истинно. В другом случае, при ложности общего суждения «Все студенты - птицы», подчиненное ему частное суждение тоже будет ложным: «Некоторые студенты - птицы». Ложность подчиняющихся частных суждений (I или О) всегда определяет ложность и соответствующих им общих суждений (А или Е). Истинность же частных — неопределенность общих: те могут быть в конкретных по содержанию случаях как истинными, так и ложными: «Некоторые студенты есть спортсмены» — истинное частное суждение. Общее же суждение «Все студенты есть спортсмены» будет ложным. Другой случай: истинное частное суждение «Некоторые студенты не есть птицы» и истинное же общее суждение «Все студенты не есть птицы». Зато ложность любого частного суждения («Некоторые студенты не есть учащиеся» или «Некоторые студенты есть птицы») всегда влечет ложность и соответствующего им общего суждения («Все студенты не есть учащиеся» или «Все студенты есть птицы»). Зная отношения между простыми категорическими суждениями (ориентируясь по логическому квадрату), легко составить сводную таблицу зависимости истинности того или иного суждения от истинности или ложности исходного. При истинности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет ложно, частноотрицательное суждение (О) тоже будет ложно, частноутвердительное (I) — истинно. При ложности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет неопределенным, частноотрицательное (О) будет истинным, частноутвердитсльное (I) — неопределенным. При истинности общеотрицательного суждения (Е) общеутвердительное (А) будет ложно, частноутвердительное (I) — тоже ложно, частноотрицательное (О) — истинно. При ложности общеотрицательного суждения (Е) общеутвердительное (А) — неопределенно, частноутвердительное (I) — истинно, частноотрицательное (О) — неопределенно. При истинности частноутвердительного суждения (I) общеутвердительное (А) — неопределенно, общеотрицательное (Е) — ложно, частноотрицательное (О) — неопределенно. При ложности частноутвердительного суждения (I) общеутвердительное суждение (А) ложно, общеотрицательное (Е) — истинно, частноотрицательное (О) — истинно. При истинности частноотрицательного суждения (О) общеутвердительное (А) — ложно, общеотрицательное (Е) — неопределенно, частноутвердительное (I) — тоже неопределенно. При ложности частноотрицательного суждения (О) общеутвердительное суждение {А) — истинно, общеотрицательное (Е} — ложно, а частноутвердительное (I) — истинно.

Зная отношения между простыми категорическими суждениями (ориентируясь по логическому квадрату), легко составить сводную таблицу зависимости истинности того или иного суждения от истинности или ложности исходного. При истинности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет ложно, частноотрицательное суждение (О) тоже будет ложно, частноутвердительное (I) — истинно. При ложности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет неопределенным, частноотрицательное (О) будет истинным, частноутвердитсльное (I) — неопределенным. При истинности общеотрицательного суждения (Е) общеутвердительное (А) будет ложно, частноутвердительное (I) — тоже ложно, частноотрицательное (О) — истинно. При ложности общеотрицательного суждения (Е) общеутвердительное (А) — неопределенно, частноутвердительное (I) — истинно, частноотрицательное (О) — неопределенно. При истинности частноутвердительного суждения (I) общеутвердительное (А) — неопределенно, общеотрицательное (Е) — ложно, частноотрицательное (О) — неопределенно. При ложности частноутвердительного суждения (I) общеутвердительное суждение (А) ложно, общеотрицательное (Е) — истинно, частноотрицательное (О) — истинно. При истинности частноотрицательного суждения (О) общеутвердительное (А) — ложно, общеотрицательное (Е) — неопределенно, частноутвердительное (I) — тоже неопределенно. При ложности частноотрицательного суждения (О) общеутвердительное суждение (А) — истинно, общеотрицательное (Е) — ложно, а частноутвердительное (I) — истинно.

⇐ Предыдущая 12