Хелпикс

Главная

Контакты

Случайная статья



12. Теорема Гаусса в интегральной форме.

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒


12. Теорема Гаусса в интегральной форме.

Для вакуума: Поток вектора напряжённости электростатического поля в вакууме сквозь замкнутую поверхность (S) равен алгебраической сумме всех зарядов (свободных и связанных), находящихся внутри объема, ограниченного этой замкнутой поверхностью (S).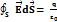             

   где 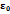- электрическая постоянная

Для среды: поток вектора электрического смещения сквозь замкнутую поверхность (S) равен свободному заряду, который находится внутри объёма, ограниченной этой замкнутой поверхностью.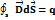        

13. Теорема Гаусса в дифференциальной форме.

 Для вакуума: Дивергенция вектора напряженности равна объемной плотности зарядов, создающих поле, деленную на электрическую постоянную )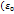    

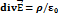
Для среды: Если заряд в данной точке поля отсутствует, то дивергенция вектора эл. смещения равна плотности свободных зарядов.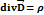   

14. Потенциал – скалярная физическая величина, равная отношению потенциальной энергии, которой обладает положительный единичный заряд, помещенный в данную точку пространства.      

 = const

15. Связь между напряженностью электрического поля и потенциалом.

Вектор напряженности электростатического поля всегда направлен в сторону убывания потенциала. (знак минус как раз это показывает) .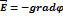

16. Уравнение Пуассона: Уравнение описывает распределение потенциалов в пространстве, если эл. поле создано системой проводников и в пространстве между проводниками имеются свободные заряды.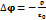    

17. Уравнение Лапласа:

Если в пространстве между проводниками свободных зарядов нет, то объёмная плотность зарядов равна нулю.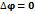   

18. Теорема Фарадея:

 1) Сумма индуцированных зарядов на внутренней поверхности проводника замкнутой оболочки равна и противоположна по знаку сумме зарядов, окруженной этой оболочкой.

2) Кулоновское поле зарядов, окруженных проводящей оболочкой, и зарядов, индуцированных на ее внутренней поверхности, равно 0 во всем внешнем пространстве.
3) Если в полости нет электрических зарядов, то электрическое поле в ней равно 0. Внешние заряды не создают в ней никакого электрического поля.

 

 


⇐ Предыдущая123456Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.