
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод интервалов
Метод интервалов часто используют при решения неравенств. Он позволяет свести решение неравенства f(x)> 0 (<, <, > ) к решению уравнения f(x) = 0.
Метод заключается в следующем:
1. Находится ОДЗ неравенства.
2. Неравенство приводится к виду f(x)> 0(<, <, > ) (т. е. правая часть переносится влево) и упрощается.
3. Решается уравнение f(x) = 0.
4. На числовой прямой отметим корни уравнения.
Равенство строгое, не закрашивать точки и закрашенных, если оно нестрогое.
5. Все точки, отмеченные на ОДЗ и ограничивающие его, разбивают это множество на так называемые интервалы знакопостоянства. На каждом таком интервале определяется знак функции f(х).
6. Ответ записывается в виде объединения отдельных множеств, на которых f{x) имеет соответствующий знак. Точки, отмеченные закрашеными кружками, в ответ входят, отмеченные пустыми - нет. Точки ОДЗ, являющиеся граничными, включаются (или не включаются) в ответ после дополнительной проверки.
Метод интервалов основан на том, что непрерывная функция f(x) может изменить знак либо в граничных точках ОДЗ, где она " разрывается", либо проходя через ноль, т. е. в точках, являющиеся корнях уравнения f(x) = 0. Ни в каких других точках перемены знака не происходит.
Пример. Решить неравенство (2x - 6)(3x + 12)(5x + 1) < 0.
Решение.
Нули функции: - 4; - 0, 2; 3.
Функция в левой части неравенства представляет собой произведение не повторяющихся множителей, значит знаки этой функции чередуются cправа на лево с " +" на " -" ....

Решение данного неравенства x 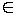 (-
(- 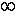 ; -4)
; -4) 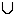 (-0, 2; 3).
(-0, 2; 3).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|