Теорема: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

§ 1 Касательная к окружности

В этом уроке мы узнаем, что подразумевается под понятиями «касательная к окружности», «отрезки касательных», докажем теорему о свойстве касательной к окружности и обратную ей теорему, являющуюся признаком касательной, познакомимся со свойством отрезков касательных, рассмотрим решение задачи по данной теме.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

На рисунке прямая р – касательная к окружности, А – точка касания.

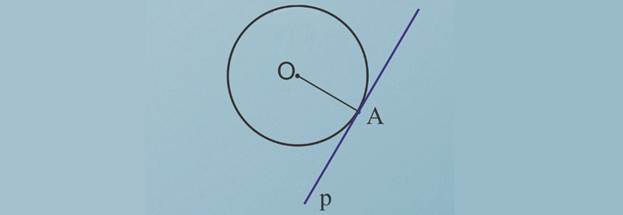
Докажем теорему о свойстве касательной к окружности.

Теорема: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Дано: окружность с центром в точке О, прямая р – касательная к окружности, А – точка касания.

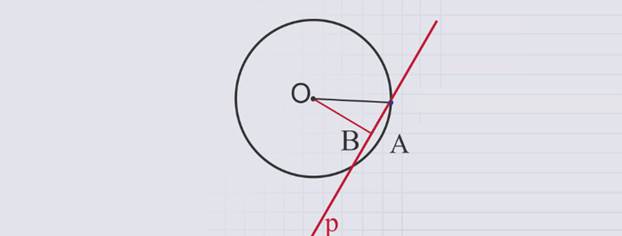
Доказать: р перпендикулярна ОА.

Доказательство: предположим, что прямая р не перпендикулярна ОА, тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из центра окружности к прямой р, меньше наклонной ОА, то расстояние от центра окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки, но это противоречит условию, что прямая р является касательной. Таким образом, предположение сделано неверно, значит, прямая р перпендикулярна к радису ОА. Что и требовалось доказать.

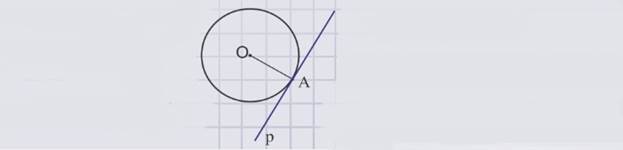
К окружности с центром в точке О проведем две касательные АВ и АС, точки В и С – точки касания. Отрезки АВ и АС называют отрезками касательных, проведенными из точки А.

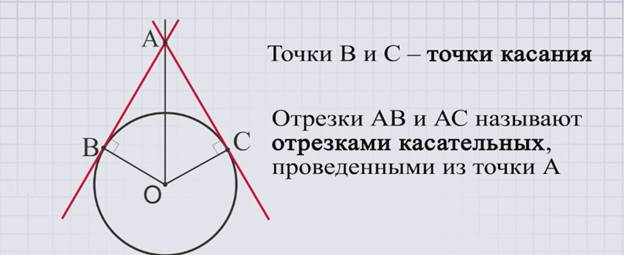
Для них справедливо свойство:

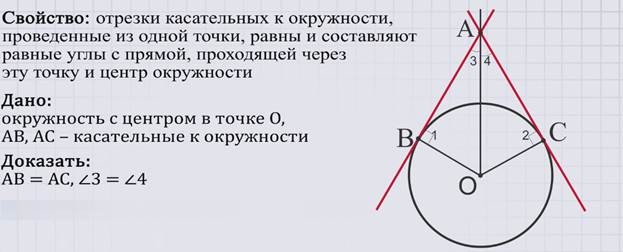
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Докажем это свойство.

Дано: окружность с центром в точке О, АВ и АС – касательные к окружности.

Доказать: АВ = АС, ∠ 3 = ∠ 4.

Доказательство: рассмотрим По теореме о свойстве касательной к окружности углы ∠ 1 и ∠ 2 прямые, поэтому 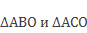- прямоугольные. Так как ОА – общая сторона и является гипотенузой для данных треугольников; ОВ = ОС, как радиусы окружности, то отсюда следует, что прямоугольные треугольники 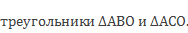равны по гипотенузе и катету. Так как треугольники равны, то АВ = АС, ∠ 3 = ∠ 4. Что и требовалось доказать.

Рассмотрим признак касательной – теорему, обратную теореме о свойстве касательной к окружности.

12 Следующая ⇒