
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
KL:=add((nuL[i]-10)^2/10,i=1..10): 'nu[L]'=nuL,'K[L]'=KL,``=evalf[6](KL);
KL: =add((nuL[i]-10)^2/10, i=1.. 10): 'nu[L]'=nuL, 'K[L]'=KL, ``=evalf[6](KL);
for alpha in Alpha do
if QChiSq8[alpha]< =KL then print('alpha'=alpha, " hypothesis L0 denied" )
else print('alpha'=alpha, " hypothesis L0 valid" ) end if end do:
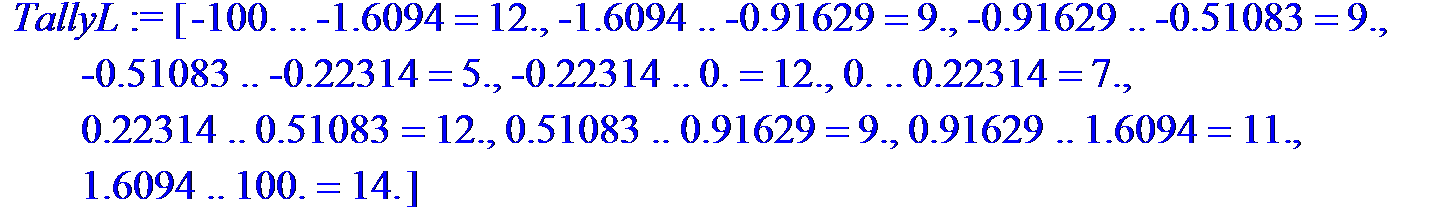





=======================================================================
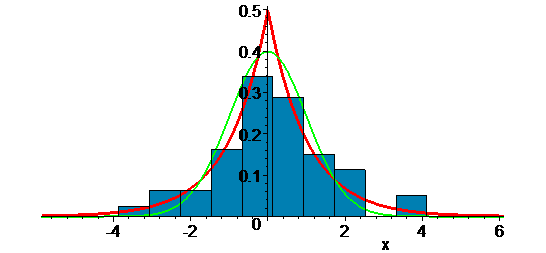
3. Histogram
___________________________________________________________________
> Tally10=evalf[6](TallyInto(xi, default, bins=10));
H10: =Histogram(xi, bincount=10): Hd: =Histogram(xi, bincount=deduce):
PfN: =plot(fN0(x), x=xi[1]-2.. xi[n]+2, thickness=2, color=green):
PfL: =plot(fL0(x), x=xi[1]-2.. xi[n]+2, thickness=3):
plots[display](H10, PfN, PfL); plots[display](Hd, PfN, PfL);


======================================================================
4. Доверительные интервалы для m, D, 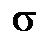
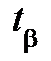 = симметричный нормальный квантиль по уровню
= симметричный нормальный квантиль по уровню 
_____________________________________________
> (t07, t095): =(Quantile(N0, 0. 5+0. 7/2, numeric), Quantile(N0, 0. 5+0. 95/2, numeric));

> I[0. 7]^`(m)`=evalf[7]([mean-t07*Sn/sqrt(n), mean+t07*Sn/sqrt(n)]),
I[0. 95]^`(m)`=evalf[7]([mean-t095*Sn/sqrt(n), mean+t095*Sn/sqrt(n)]), 'conjugate(x[n])'=evalf[7](mean);
I[0. 7]^`(D)`=evalf[7]([Sn2*(1-t07*sqrt(2/n)), Sn2*(1+t07*sqrt(2/n))]),
I[0. 95]^`(D)`=evalf[7]([Sn2*(1-t095*sqrt(2/n)), Sn2*(1+t095*sqrt(2/n))]), 'S[n]^2'=evalf[7](Sn2);
I[0. 7]^sigma=evalf[7]([Sn*sqrt(1-t07*sqrt(2/n)), Sn*sqrt(1+t07*sqrt(2/n))]),
I[0. 95]^sigma=evalf[7]([Sn*sqrt(1-t095*sqrt(2/n)), Sn*sqrt(1+t095*sqrt(2/n))]), 'S[n]'=evalf[7](Sn);
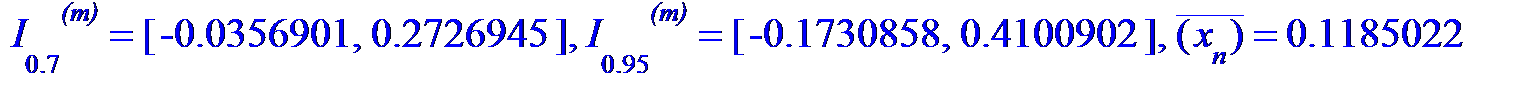
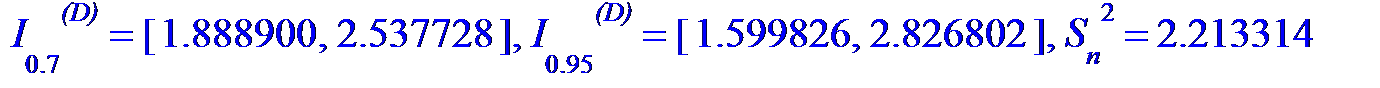
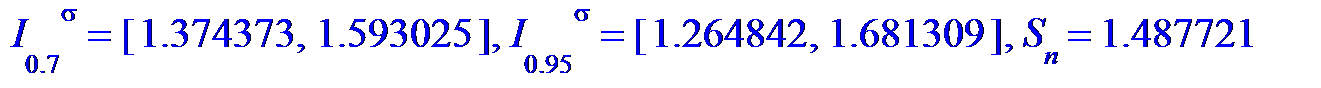
>
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|