'fN(x)'=fN(x),'fL(x)'=fL(x),'fN0(x)'=fN0(x),'fL0(x)'=fL0(x);

Стр 1 из 2Следующая ⇒

TP5-1_stats. mws

_______________________________________________

> with(Statistics):

Distribution hypothesis // //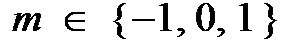

____________________________________________

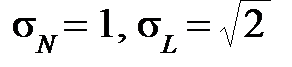
> N: =Normal(m, 1): L: =Laplace(m, 1): N0: =Normal(0, 1): L0: =Laplace(0, 1):

fN: =proc(x) '1/sqrt(2*Pi)'*exp(-(x-m)^2/2) end proc: fN0: =proc(x) '1/sqrt(2*Pi)'*exp(-x^2/2) end proc:

fL: =proc(x) 1/2*exp(-abs(x-m)) end proc: fL0: =proc(x) 1/2*exp(-abs(x)) end proc:

'fN(x)'=fN(x), 'fL(x)'=fL(x), 'fN0(x)'=fN0(x), 'fL0(x)'=fL0(x);

______________________________________________________________________

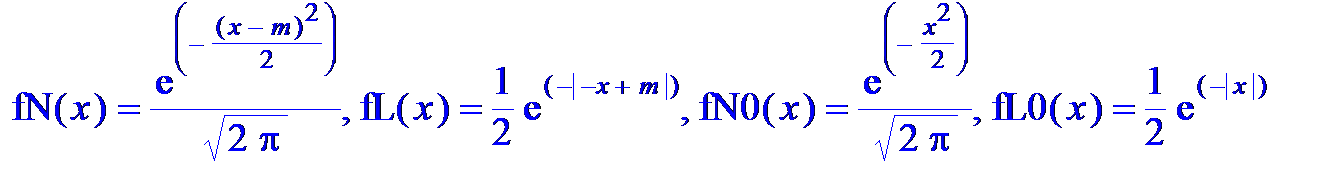
Вариационный ряд

____________________________________________________________________

> xi: =[

-3. 86052, -3. 42316, -2. 72351, -2. 49187, -2. 44700, -2. 43264, -2. 42947, -2. 18126, -2. 09994, -2. 09576,

-2. 01496, -1. 82346, -1. 39480, -1. 37066, -1. 34024, -1. 22842, -1. 17336, -1. 09060, -1. 08564, -1. 06363,

-1. 05431, -0. 86005, -0. 82328, -0. 69201, -0. 68549, -0. 63250, -0. 54215, -0. 54101, -0. 53535, -0. 51468,

-0. 46022, -0. 41540, -0. 35836, -0. 27503, -0. 26973, -0. 21221, -0. 18923, -0. 15780, -0. 15454, -0. 14784,

-0. 14091, -0. 11861, -0. 06847, -0. 03430, -0. 02684, -0. 02232, -0. 00592, 0. 00951, 0. 02006, 0. 06044,

0. 06288, 0. 09984, 0. 18579, 0. 21083, 0. 24306, 0. 25950, 0. 26220, 0. 26627, 0. 32471, 0. 35281,

0. 40669, 0. 44162, 0. 44209, 0. 45376, 0. 48010, 0. 50746, 0. 54041, 0. 58663, 0. 58826, 0. 63158,

0. 66397, 0. 67599, 0. 78838, 0. 82336, 0. 89361, 1. 00428, 1. 19282, 1. 22118, 1. 26202, 1. 30187,

1. 36321, 1. 41485, 1. 42867, 1. 46458, 1. 54869, 1. 55692, 1. 71489, 1. 73556, 1. 85562, 1. 88241,

2. 00751, 2. 03773, 2. 07349, 2. 35922, 2. 40562, 2. 41055, 3. 35088, 3. 50370, 4. 06305, 4. 11855 ]:

n: =nops(xi); [seq(j=xi[j], j=1.. n)];

=====================================================================

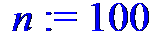
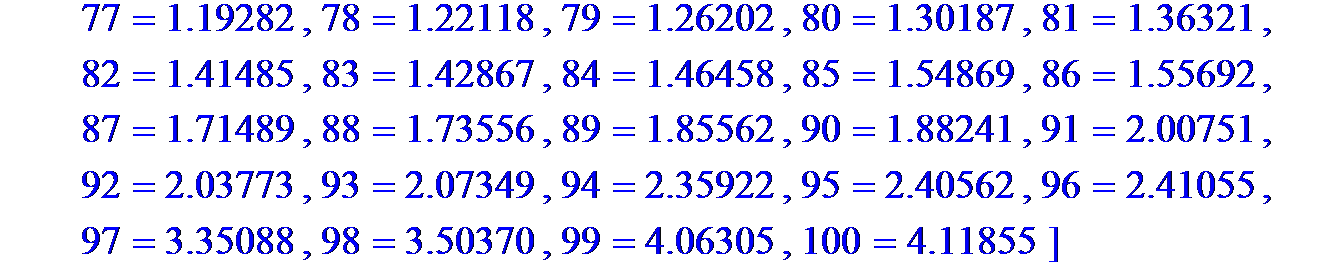
1. Выборочная медиана 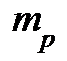и среднее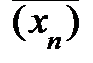

Выборочное средне-квадрат. отклонение 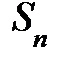, оценка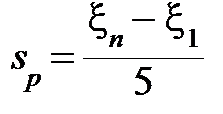

_________________________________________________

> mean: =convert(xi, `+`)/n: Sn2: =sum((xi[j]-mean)^2, j=1.. n)/n: Sn: =sqrt(Sn2):

'm[p]'=evalf[6]((xi[n/2]+xi[n/2+1])/2), conjugate('x[n]')=evalf[6](mean), m=0;

'S'['n']^2=evalf[6](Sn2), 'S'['n']=evalf[6](Sn), 's[p]'=evalf[6]((xi[n]-xi[1])/5);

===========================================================

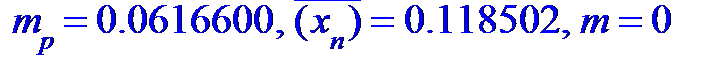
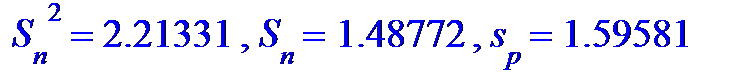
2. Quantiles for N0, L0, ChiSquare(9)

_________________________________________________

> QN0: =[-100, seq(Quantile(N0, j/10, numeric), j=1.. 9), 100]: nQ: =11: 'QN0'=evalf[6](QN0);

QL0: =[-100, seq(Quantile(L0, j/10, numeric), j=1.. 9), 100]: 'QL0'=evalf[6](QL0);

Alpha: =[0. 5, 0. 2, 0. 05, 0. 025]: ## Уровни значимости

QChiSq9: =table([seq(alpha=Quantile(ChiSquare(9), 1-alpha, numeric), alpha=Alpha)]):

'QChiSq9'=evalf[8](sort(op(op(QChiSq9)), (a, b)-> lhs(a)> lhs(b)));

QChiSq8: =table([seq(alpha=Quantile(ChiSquare(8), 1-alpha, numeric), alpha=Alpha)]):

'QChiSq8'=evalf[8](sort(op(op(QChiSq8)), (a, b)-> lhs(a)> lhs(b)));

________________________________________________________________________

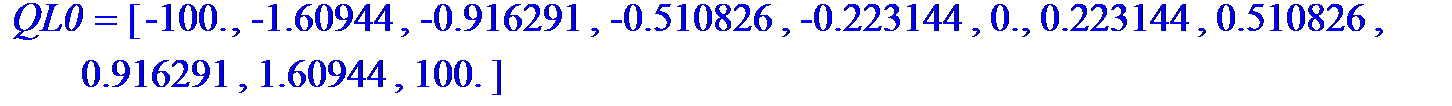
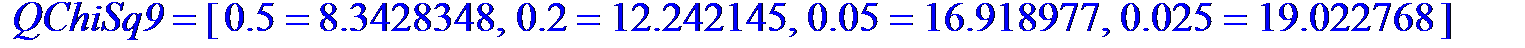
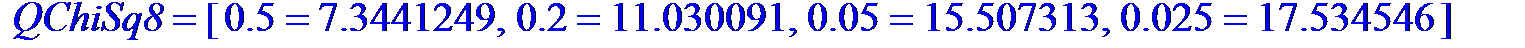
Интервальные группировки в условиях N0;

ChiSq-criterion: ,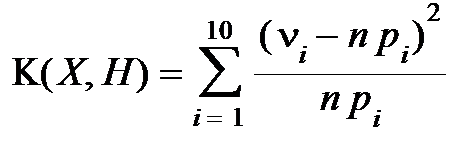

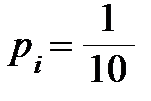
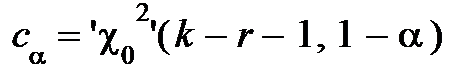Правило: если 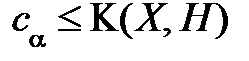, то гипотеза H отклоняется.

______________________________________

> TallyN: =evalf[5](TallyInto(xi, [seq(QN0[j].. QN0[j+1], j=1.. nQ-1)])); kN: =map(t-> floor(op(2, t)), TallyN):

KN: =add((kN[i]-10)^2/10, i=1.. 10): 'kN'=kN, 'K[N]'=KN, ``=evalf[6](KN);

for alpha in Alpha do

if QChiSq8[alpha]< =KN then print('alpha'=alpha, " hypothesis N0 denied" )

else print('alpha'=alpha, " hypothesis N0 valid" ) end if end do:

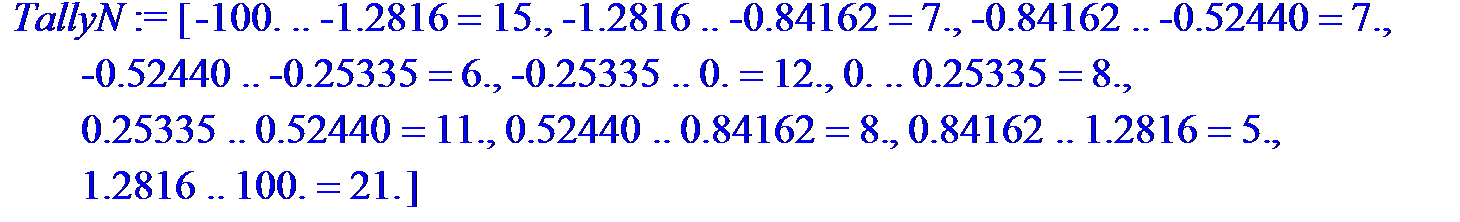
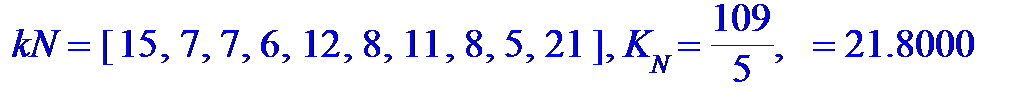
Интервальные группировки в условиях L0

_____________________________________

> TallyL: =evalf[5](TallyInto(xi, [seq(QL0[j].. QL0[j+1], j=1.. nQ-1)])); nuL: =map(t-> floor(op(2, t)), TallyL):

12 Следующая ⇒