
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2. Основные свойства логарифмов.
2. Основные свойства логарифмов.
При работе с логарифмами применяются их следующие свойства.
При любом 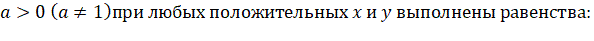
1. 
2. 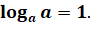
3. 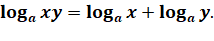
4. 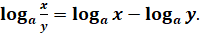
5. 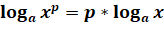 , для любого действительного p.
, для любого действительного p.
Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы.
6. Формула перехода к новому основанию:
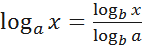 x> 0, a> 0, a≠ 1, b> 0, b≠ 1
x> 0, a> 0, a≠ 1, b> 0, b≠ 1
С помощью формулы перехода можно найти значение логарифма с произвольным основанием, имея таблицы логарифмов, составленных для какого-нибудь одного основания b. Наиболее употребительны таблицы десятичных и натуральных логарифмов.
3. Десятичные и натуральные логарифмы.
В математике принято следующее сокращение:
log10 a= lgа- десятичный логарифм числа а (буква «о» пропускается, а основание 10 не ставят).
loge а= ln а - натуральный логарифм числа а. «е» - это такое иррациональное число, равное 2, 7 (буква «о» пропускается, а основание «е» не ставят).
Рассмотрим примеры:
lg 10=1; lg 1=0
ln e=1; ln 1=0.
Формула 6 потребуется при вычислении логарифма по калькулятору.
Возьмем пример: log3 7 = lg7 / lg3. В калькуляторе можно вычислить только десятичный и натуральный логарифм. Вводим цифру 7 и нажмем кнопку «лог», также вводим цифру 3 и нажмем кнопку «лог», делим верхнее значение на нижнее и получаем ответ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|