Хелпикс

Главная

Контакты

Случайная статья



Типові задачі. I. Арифметична прогресія. 1. Довести, що послідовність  - арифметична прогресія.. 2.Дано арифметичну прогресію 2,5,8,.. Знайти сотий член.. 3.Відомо 2 члени арифметичної прогресії: . Знайти .. 4. Відомо 2 члени арифметичної прогресії : =7,

Стр 1 из 4Следующая ⇒


  Типові задачі

I. Арифметична прогресія

1. Довести, що послідовність  - арифметична прогресія.

Розв’язання:

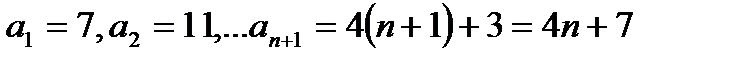
Знайдемо різницю

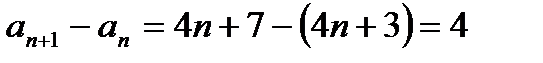- отже, за означенням, це арифметична прогресія.

2. Дано арифметичну прогресію 2, 5, 8,.. Знайти сотий член.

Розв’язання:

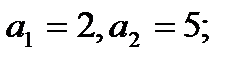
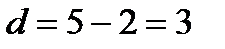
Знайдемо n-ий член


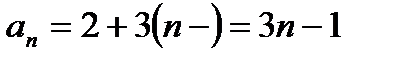
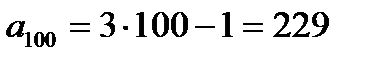
Відповідь: .

3. Відомо 2 члени арифметичної прогресії: . Знайти.

Розв’язання:

Використаємо формулу n-го члена

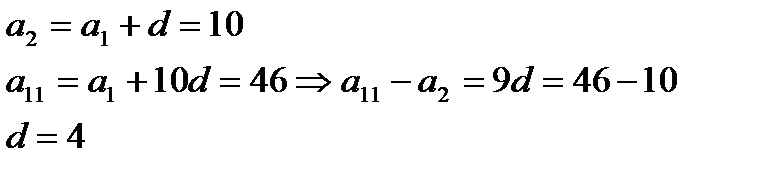
Далі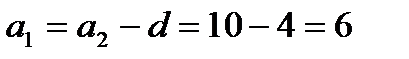

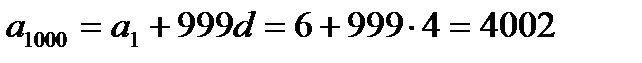
Відповідь: .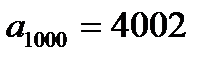

4. Відомо 2 члени арифметичної прогресії: =7, =19. Знайти.

Розв’язання: За формулою n-го члена

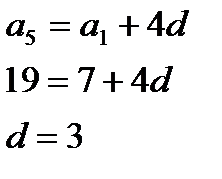
Звідси знайдемо

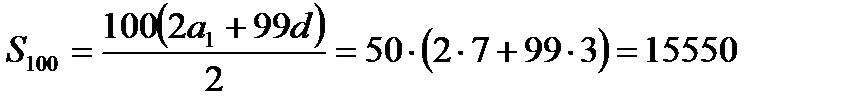
Відповідь: 15 550.

5. Знайти суму всіх тризначних чисел, які діляться на 7.

Розв’язання:

Найменше тризначне число, яке ділиться на 7=105, найбільше = 994. Всі тризначні числа, які діляться на 7, утворюють арифметичну прогресію: 105, 112, 119, …, 994, у якої

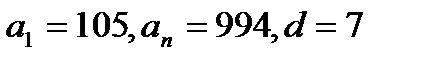, згідно формули n-го члена

 

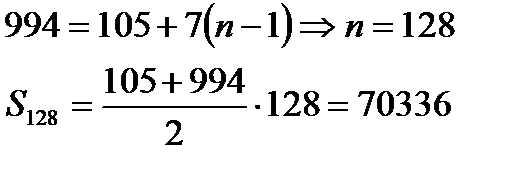
Відповідь: 70 336.

II. Геометрична прогресія

1. Послідовність задано формулою. Довести, що це геометрична прогресія.

Доведення:

Маємо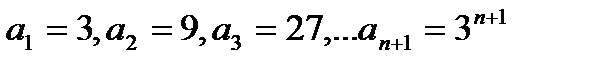

Знаходимо 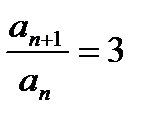. Отже, за означенням – це геометрична прогресія.

2. Між 1, 81 знайти 3 числа, які б разом з даними утворювали геометричну прогресію.

Розв’язання:

Нехай 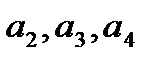- шукані числа. Маємо геометричну прогресію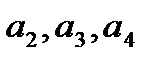: 1, . 81.

Згідно з формулою n-го члена

81=1 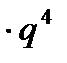, звідки .

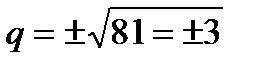Маємо 2 випадки:

а)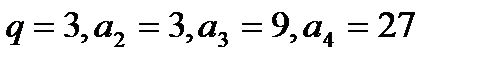

б) .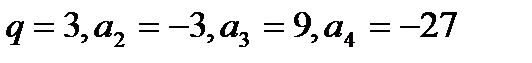

3. Чотири числа утворюють геометричну прогресію. Якщо до двох перших додати 1, то до третього і четвертого додати 4 і 13 відповідно, то дістанемо арифметичну прогресію. Знайти ці числа.

 Розв’язання:

Нехай шукані числа 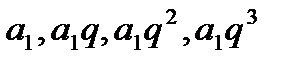. Тоді числ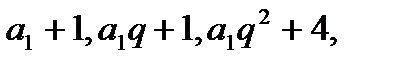а та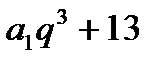

Утворюють арифметичну прогресію. Використаємо характеристичну властивість арифметичної прогресії, дістанемо систему рівнянь:

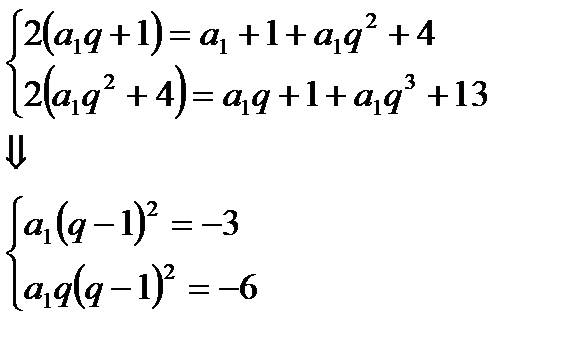
Так-як 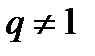, поділимо перше і друге рівняння і дістанемо і дістанемо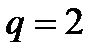

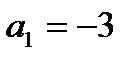, отже шукані числа -3, -6, -12. -24.

III Нескінченно спадна геометрична прогресія:


1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.