1 ПРИЕМ.. М2И ч.1 стр. 33,34

⇐ ПредыдущаяСтр 2 из 2

1 ПРИЕМ.

Вычитание по частям.

Например, 12-5

1. Сначала вычитают столько, чтобы получилось 10:

12-2=10

2. Вспоминаем, что 5 это 2 и 3. 2 уже вычли, значит, надо вычесть еще3

3. Вычитаем 3 из 10:

10-3=7

Т. О. приема: 1. Разрядный состав двузначного числа;

2. Состав чисел в пределах 10;

3. Состав числа 10.

Модели приема:

12 - 5 = 7 12 – 5 = 7

2 3 12 - 2- 3 = 7

При объяснении опираемся на абак такой же, как при сложении.

2 ПРИЕМ.

Т. О 1. Знание состава чисел в пределах 20.

2. Связь между слагаемыми и суммой, т. е. правило: если из суммы вычесть одно слагаемое, то получится другое слагаемое.

Например, 12-5

1. Вспоминаем, что 12 это 5 и 7.

2. Мы знаем, что если из суммы 12 вычесть одно слагаемое 5, то получим второе слагаемое 7.

12 – 5 = 7 12 – 5 =

12 = 5 + 7

5 7 12 – 5 = 7

После того, как изучили оба приема (1-2 урока) переходят к их применению для случаев вычитания с переходом через разряд. Дети могут пользоваться любым приемом. Учитель чередует способы объяснения. Эти случаи сложны для запоминания, поэтому их разбили на группы и изучают несколько уроков.

Стр. 82 11 - (2, 3, 4, 5, 6, 7, 8, 9). Эти случаи подробно разбирают, выписывают на доску и в тетрадь и предлагают заучить.

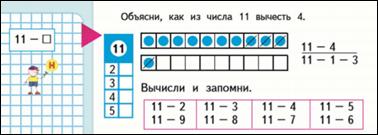
Стр. 83 12 - 3, 4, 5, 6, 7, 8, 9

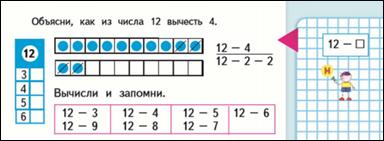
Стр. 84 13 - 4, 5…9

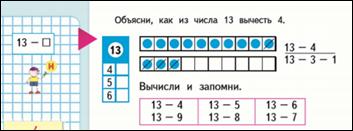
Стр. 85 14 - 5, 6…9

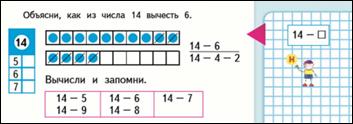
Стр. 86 15 - 6, 7…9

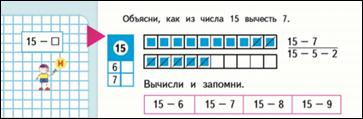
Стр. 87 16 - 7, 8…9

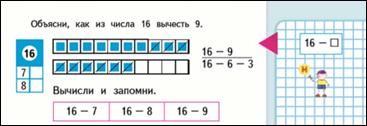
Стр. 88 17, 18 - 8, 9.

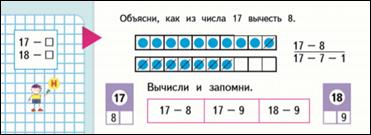
Сводная таблица вычитания не составляется, пользуются таблицей сложения.

К концу темы дети должны знать все случаи сложения и вычитания в пределах 20 наизусть.

Для заучивания случаев на каждом уроке используют работу с карточками,

математические диктанты, дидактические игры, самостоятельные работы и т. п.

По программе Н. Б. Истоминой эта тема изучается во 2 классе. Сначала детям показывают прием сложения с переходом через десяток на моделях.

М2И ч. 1 стр. 33, 34

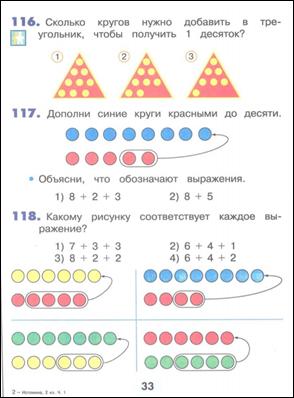
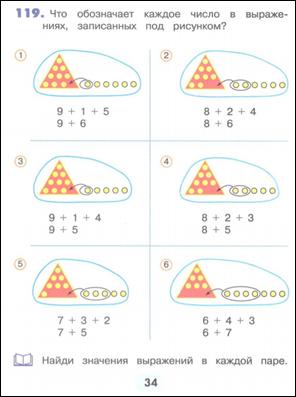
После этого рассматривают и заучиваютсостав каждого числа от 11 до 19 отдельно.

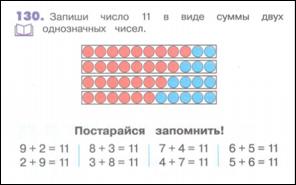
М2И ч. 1 с. 38

М2И ч. 1 с. 45

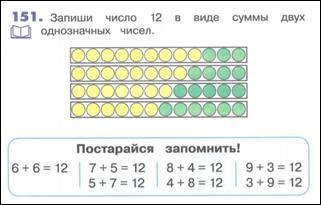
Вычитание рассматривают как действие обратное сложению, опираясь на второй прием вычитания, т. е. на правило: если из суммы вычесть одно слагаемое, то получится другое слагаемое. Этот прием основной в этом учебнике, хотя первый прием вычитания тоже используют.

Вопрос 16.

В этом уроке научимся складывать однозначные числа, переходя через десяток.

Любит порядок мальчик Николка.

Диски свои расставил на полки:

Девять дисков на одной

И четыре на другой.

Сколько дисков, сосчитай.

И ответ скорее дай!

Какое решение у этой задачи?

Правильно, 9 + 4.

9 и 4 – это слагаемые, нам нужно найти сумму этих чисел.

Но как же сосчитать?

Посмотрите на натуральный ряд однозначных чисел, которые стоят в порядке возрастания.

1, 2, 3, 4, 5, 6, 7, 8, 9.

Составим из этих чисел суммы, равные 10:

Чтобы сложить числа 9 и 4, необходимо дополнить одно из слагаемых до 10.

К первому слагаемому 9 прибавим 1 – часть второго слагаемого.

От второго слагаемого осталось 3.

К 10 прибавить 3 получим 13.

Ответ: 13 дисков было у Николки.

Сложить числа 9 и 4 можно было по-другому, дополнив до 10 не первое, а второе слагаемое.

К 4 прибавить 6, будет 10.

От первого слагаемого осталось 3.

Прибавим этот остаток к 10, получится 13.

Как видите, результат тот же.

Но легче было вычислять первым способом, потому что удобнее складывать большее с меньшим.

Рассмотрим другой пример.

Найдем сумму 5 + 7.

Используя переместительное свойство сложения: от перестановки мест слагаемых сумма не изменяется, поменяем слагаемые местами 7 + 5.

Дополним первое слагаемое 7 до 10, разбив второе слагаемое на части, получим:

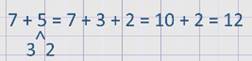
Ответ: 12

Итак, важно запомнить:

1. Чтобы сложить однозначные числа с переходом через десяток, необходимо одно из слагаемых разбить на части, дополнив другое слагаемое до десятка.

2. Легче прибавлять к большему числу меньшее, используя переместительное свойство сложения.

⇐ Предыдущая 12