
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1) Полином наилучшего равномерного приближения для непрерывной функции.
Задание 3.
1) Полином наилучшего равномерного приближения для непрерывной функции.
Пусть 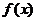 непрерывна на
непрерывна на 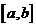 . Полином
. Полином 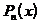 будет полиномом наилучшего приближения для функции
будет полиномом наилучшего приближения для функции 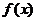 на
на 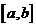 , если
, если 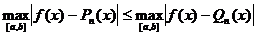 для всех
для всех 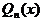 , являющихся полиномами степени п. Для построения полинома наилучшего приближения воспользуемся теоремой Чебышева об альтернансе: Полином
, являющихся полиномами степени п. Для построения полинома наилучшего приближения воспользуемся теоремой Чебышева об альтернансе: Полином 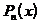 будет полиномом наилучшего приближения для функции
будет полиномом наилучшего приближения для функции 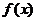 на
на 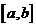 , если на
, если на 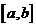 найдется
найдется 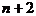 точки
точки 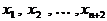 , так, что
, так, что  , а знаки этой разности в соседних точках чередуются. Точки
, а знаки этой разности в соседних точках чередуются. Точки 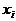 называются точками альтернанса.
называются точками альтернанса.
Многочлен 1-й степени. Пусть 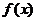 – выпуклая, положительная на
– выпуклая, положительная на 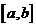 . Построим
. Построим 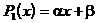 . В силу выпуклости
. В силу выпуклости 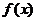 разность
разность 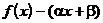 может иметь только одну внутреннюю точку экстремума (производная может обратиться в 0 только в одной точке). Обозначим ее d. Значит, точки альтернанса – a, d, b. Получаем уравнения для определения
может иметь только одну внутреннюю точку экстремума (производная может обратиться в 0 только в одной точке). Обозначим ее d. Значит, точки альтернанса – a, d, b. Получаем уравнения для определения 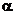 и
и 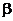 :
:
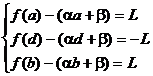 (*)
(*)
Из 3-го уравнения вычитаем 1-е: 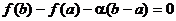 . Отсюда
. Отсюда 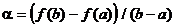 . Запишем уравнение касательной к
. Запишем уравнение касательной к 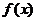 в точке x=d:
в точке x=d: 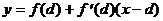 . Продифференцируем разность
. Продифференцируем разность 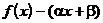 , получим
, получим 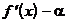 . Эта функция в т. d обращается в 0. Значит,
. Эта функция в т. d обращается в 0. Значит, 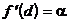 . Т. е. a – угловой коэффициент касательной. Теперь запишем хорду, соединяющую точки
. Т. е. a – угловой коэффициент касательной. Теперь запишем хорду, соединяющую точки 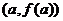 и
и 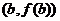 :
: 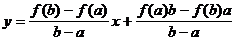 . Значит, касательная параллельна этой хорде. Теперь сложим 1-е и 2-е уравнения в (*):
. Значит, касательная параллельна этой хорде. Теперь сложим 1-е и 2-е уравнения в (*): 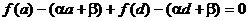 . Отсюда
. Отсюда  . Это означает, что искомая прямая лежит посередине между хордой и касательной и параллельна им.
. Это означает, что искомая прямая лежит посередине между хордой и касательной и параллельна им.
Задание. Построить полином наилучшего равномерного приближения 1-й степени для указанной в задании функции на промежутке 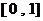 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|