Министерство связи и массовых коммуникаций

Стр 1 из 2Следующая ⇒

Министерство связи и массовых коммуникаций

Федеральное агентство связи

Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования

«Поволжская государственный университет телекоммуникаций и информатики»

Кафедра высшей математики

Одобрено Советом ФБТО 17. 04. 13,

протокол №8

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КОНТРОЛЬНОЙ РАБОТЫ 5 ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ

ДЛЯ СТУДЕНТОВ ОЧНОЙ И ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

Авторы-составители

профессор, д. ф. м. -н. Блатов И. А.

доцент, к. ф. -м. н Китаева Е. В.

доцент, к. ф. м. -н. Шевченко Г. Н.

Рецензент

профессор, д. ф. м. -н. Асташкин С. В.

Самара, 2013

ВВЕДЕНИЕ

В настоящее время математические методы широко используются для решения самых разнообразных задач науки, техники и экономики. Значение этих методов существенно возросло в связи с массовым применением компьютеров во всех сферах деятельности.

Программа курса математики составлена в объеме, необходимом для изучения общенаучных, общеинженерных и специальных дисциплин и развития навыков, требуемых для применения математических методов в практике работы инженера.

Общий курс математики, изучаемый студентами-заочниками ПГАТИ а течение обучения в академии состоит из аналитической геометрии и линейной алгебры, математического анализа, элементов теории вероятностей и математической статистики, дискретной математики.

В первом семестре изучается аналитическая геометрия и линейная алгебра, первая часть курса математического анализа.

При изучении этих разделов рекомендуется использовать следующую литературу:

1. Логинов Б. М. Введение в дискретную метематику. Калуга, 2008.

2. Москинова Г. И. Дискретная математика. Математика для менеджере в примерах и упражнениях. М.: Логос, 2010.

3. Новиков Ф. А. Дискретная математика для программистов. СПб, Питер, 2007.

Программа экзамена по дискретной математике

1. Понятие множества. Операции над множествами. Диаграммы Эйлера-Венна.

2. Мощность множества. Счетные множества.

3. Прямое произведение множеств. Понятие n-местного отношения.

4. Соответствия между множествами. Функции. Инъекция, сюръекция, биекция.

5. Отношения. Бинарные отношения. Свойства отношений.

6. Отношение эквивалентности. Связь между отношением эквивалентности и разбиением множества.

7. Отношения частичного и строгого порядка.

8. Булевы функции одной и двух переменных.

9. Булевы функции. Способы задания. Существенные и фиктивные переменные.

10. Булевы формулы. Свойства логических операций.

11. Разложение булевой функции по переменным. Алгоритмы построения совершенной дизъюнктивной нормальной формы и совершенной конъюнктивной нормальной формы.

12. Свойства суммы по модулю 2. Алгоритм построения полинома Жегалкина.

13. Замкнутые классы функций. Классы T₀, T₁, S, M, L.

14. Функционально полные системы. Теорема о функциональной полноте двух систем функций. Теорема Поста.

15. Схемы из функциональных элементов.

16. Основные задачи комбинаторики. Правило суммы. Правило произведения.

17. Формулы числа перестановок, размещений и сочетаний без повторений и с повторениями.

18. Формула включения и исключения. Задача о беспорядках.

19. Понятие рекуррентного соотношения. Линейные рекуррентные соотношения. Метод решения.

20. Графы. Основные понятия и определения. Изоморфизм графов.

21. Степени и полустепени вершин графа. Свойства.

22. Построение графа с заданным набором степеней вершин. Необходимое и достаточное условие существования. Алгоритм построения.

23. Матрица смежности. Матрица инцидентности. Свойства.

24. Маршруты, цепи, циклы. Связность. Метрические характеристики графа.

25. Алгоритм отыскания кратчайших путей в графе (волновой метод).

26. Планарность графов. Формула Эйлера.

27. Конечные автоматы. Основные понятия. Способы задания конечных автоматов.

28. Понятие алгоритма. Основные требования к алгоритмам.

29. Машина Тьюринга. Структура машины Тьюринга. Программа для машины Тьюринга.

30. Рекурсивные функции.

Варианты контрольной работы обновляются ежегодно и размещаются на сайте академии psati. ru. Номер Вашего варианта совпадает с последними тремя цифрами Вашей зачетной книжки.

ПРИМЕРНЫЙ ВАРИАНТ КОНТРОЛЬНОЙ РАБОТЫ N5 С РЕШЕНИЕМ

Задача 1

Определить, являются ли формулы f и g

эквивалентными.

f(x, y, z)=((y~x)─ > (z │ x))& ((zVx)& (z+y))

g(x, y, z)=((x─ > y)V(z─ > x))& ((z─ > y)~(xVy))

Примечание:

& - конъюнкция

V - дизъюнкция

~ - эквивалентность

─ > - импликация

+ - сложение по модулю 2

│ - штрих Шеффера

│ - стрелка Пирса

Решение.

f(x, y, z)=((y~x)─ > (z │ x))& ((zVx)& (z+y))

g(x, y, z)=((x─ > y)V(z─ > x))& ((z─ > y)~(xVy))

Используя таблицы истинности для элементарных

булевых функций, получим:

┌ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ┐

│ x y z│ y~x│ z │ x│ (y~x)─ > (z │ x)│ zVx│ z+y│ (zVx)& (z+y)│ f │

│ │ │ v │ v │ │ │ │ │

├ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ┤

│ 0 0 0│ 1 │ 1 │ 1 │ 0 │ 0 │ 0 │ 0 │

│ 0 0 1│ 1 │ 0 │ 0 │ 1 │ 1 │ 1 │ 1 │

│ 0 1 0│ 0 │ 1 │ 1 │ 0 │ 1 │ 0 │ 0 │

│ 0 1 1│ 0 │ 0 │ 1 │ 1 │ 0 │ 0 │ 0 │

│ 1 0 0│ 0 │ 0 │ 1 │ 1 │ 0 │ 0 │ 0 │

│ 1 0 1│ 0 │ 0 │ 1 │ 1 │ 1 │ 1 │ 1 │

│ 1 1 0│ 1 │ 0 │ 0 │ 1 │ 1 │ 1 │ 1 │

│ 1 1 1│ 1 │ 0 │ 0 │ 1 │ 0 │ 0 │ 1 │

└ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ┘

┌ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ┐

│ x y z│ x─ > y│ z─ > x│ (x─ > y)V(z─ > x)│ z─ > y│ xVy│ (z─ > y)~(xVy)│ g │

│ │ │ │ │ │ │ │ │

├ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ┤

│ 0 0 0│ 1 │ 1 │ 1 │ 1 │ 0 │ 0 │ 1 │

│ 0 0 1│ 1 │ 0 │ 1 │ 0 │ 0 │ 1 │ 1 │

│ 0 1 0│ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │

│ 0 1 1│ 1 │ 0 │ 1 │ 1 │ 1 │ 1 │ 1 │

│ 1 0 0│ 0 │ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │

│ 1 0 1│ 0 │ 1 │ 1 │ 0 │ 1 │ 0 │ 1 │

│ 1 1 0│ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │

│ 1 1 1│ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │ 1 │

└ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ┘

Из таблиц истинности следует, что формулы f и g

не эквивалентны.

Задача 2

Для булевой функции, заданной вектором значений (11100111),

определить:

1) существенные и фиктивные переменные;

2) совершенную дизъюнктивную нормальную форму;

3) совершенную конъюнктивную нормальную форму;

4) полином Жегалкина двумя способами;

5) принадлежность классам T0, T1, S, M, L

Решение.

f(x, y, z) = (11100111)

1) Построим таблицу истинности данной булевой функции

┌ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┐

│ N │ x y z f(x, y, z) │

├ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┤

│ 1 │ 0 0 0 1 │

│ 2 │ 0 0 1 1 │

│ 3 │ 0 1 0 1 │

│ 4 │ 0 1 1 0 │

│ 5 │ 1 0 0 0 │

│ 6 │ 1 0 1 1 │

│ 7 │ 1 1 0 1 │

│ 8 │ 1 1 1 1 │

└ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ┘

Переменная x булевой функции f(x, y, z) называется

фиктивной, если имеет место равенство

f(0, y, z) = f(1, y, z)

при любых значениях переменных y и z.

В противном случае переменная x называется существенной.

Наборы значений переменных в последнем равенстве называются

соседними по переменной x.

Проверим является ли переменная x существенной или фиктивной.

Рассмотрим значения функции на наборах, соседних по переменной x:

f(0, 0, 0)=1 f(1, 0, 0)=0

f(0, 0, 1)=1 f(1, 0, 1)=1

f(0, 1, 0)=1 f(1, 1, 0)=1

f(0, 1, 1)=0 f(1, 1, 1)=1

Так как не на всех наборах, соседних по переменной x, совпадают

значения функции, то переменная x является существенной.

Проверим является ли переменная y существенной или фиктивной.

Рассмотрим значения функции на наборах, соседних по переменной y:

f(0, 0, 0)=1 f(0, 1, 0)=1

f(0, 0, 1)=1 f(0, 1, 1)=0

f(1, 0, 0)=0 f(1, 1, 0)=1

f(1, 0, 1)=1 f(1, 1, 1)=1

Так как не на всех наборах, соседних по переменной y, совпадают

значения функции, то переменная y является существенной.

Проверим является ли переменная z существенной или фиктивной.

Рассмотрим значения функции на наборах, соседних по переменной z:

f(0, 0, 0)=1 f(0, 0, 1)=1

f(0, 1, 0)=1 f(0, 1, 1)=0

f(1, 0, 0)=0 f(1, 0, 1)=1

f(1, 1, 0)=1 f(1, 1, 1)=1

Так как не на всех наборах, соседних по переменной y, совпадают

значения функции, то переменная z является существенной.

Совершенная дизъюнктивная нормальная форма для данной булевой

функции f(x, y, z) имеет вид:

_ _ _ _ _ _ _ _ _

f(x, y, z) = x∙ y∙ z V x∙ y∙ z V x∙ y∙ z V x∙ y∙ z V x∙ y∙ z V x∙ y∙ z.

Совершенная конъюнктивная нормальная форма для данной булевой

функции f(x, y, z) имеет вид:

_ _ _

f(x, y, z) = (x V y V z)∙ (x V y V z).

Первый способ.

Полином Жегалкина для любой булевой функции от

трех переменных имеет вид

f(x, y, z) = a0 + a1∙ x + a2∙ y + a3∙ z + a4∙ x∙ y +

(1)

+ a5∙ x∙ z + a6∙ y∙ z + a7∙ x∙ y∙ z,

где a0, a1, a2, a3, a4, a5, a6, a7 є {0, 1},

значок " +" обозначает сложение по модулю 2.

Коэффициенты a0, a1,..., a7 будем находить, последовательно

подставляя в формулу (1) наборы значений переменных:

f(0, 0, 0) = a0 = 1

f(0, 0, 1) = a0 + a3 = 1

f(0, 1, 0) = a0 + a2 = 1

f(0, 1, 1) = a0 + a2 + a3 + a6 = 0 (2)

f(1, 0, 0) = a0 + a1 = 0

f(1, 0, 1) = a0 + a1 + a3 + a5 = 1

f(1, 1, 0) = a0 + a1 + a2 + a4 = 1

f(1, 1, 1) = a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7 = 1.

Из системы уравнений (2) находим

a0 = 1

a1 = 1 + 0 = 1

a2 = 1 + 1 = 0

a3 = 1 + 1 = 0

a4 = 1 + 1 + 0 + 1 = 1

a5 = 1 + 1 + 0 + 1 = 1

a6 = 1 + 1 + 1 + 0 = 1

a6 = 1 + 1 + 1 + 0 + 0 + 1 + 1 + 1 = 0

Таким образом

f(x, y, z) = 1 + x + x∙ y + x∙ z + y∙ z.

Второй способ.

В совершенной дизъюнктивной нормальной форме булевой

функции дизъюнкции заменим суммами по модулю 2

_ _ _ _ _ _ _ _ _

f(x, y, z) = x∙ y∙ z + x∙ y∙ z + x∙ y∙ z + x∙ y∙ z + x∙ y∙ z + x∙ y∙ z.

Заменим отрицание по формуле x = x+1

f(x, y, z) = (x+1)∙ (y+1)∙ (z+1) + (x+1)∙ (y+1)∙ z + (x+1)∙ y∙ (z+1) +

+ x∙ (y+1)∙ z + x∙ y∙ (z+1) + x∙ y∙ z.

Раскрывая скобки и учитывая, что x+x = 0, получаем

полином Жегалкина

f(x, y, z) = 1 + x + x∙ y + x∙ z + y∙ z.

Класс T0 функций, сохраняющих нуль

Так как

f(0, 0, 0) = 1, то

f(x, y, z) є T0.

Класс T1 функций, сохраняющих единицу

Так как

f(1, 1, 1) = 1, то f(x, y, z) є T1.

Класс S самодвойственных функций составляют функции, на

противоположных наборах принимающие противоположные значения,

Так как

f(0, 0, 0) = 1 f(1, 1, 1) = 1, то

f(x, y, z) є S.

Класс M монотонных функций

f(x, y, z) є M, так как f(0, 0, 0)> f(0, 1, 1)

Класс L линейных функций составляют функции, которые

представляются полиномом Жегалкина первой степени.

f(x, y, z) є L, так как

f(x, y, z) = 1 + x + x∙ y + x∙ z + y∙ z.

Задача 3

По заданной матрице смежности построить неориентированный граф,

составить таблицу степеней вершин, матрицу инцидентности, таблицу

расстояний и условных радиусов, найти радиус и центр графа.

║ 0 1 0 0 0 0 0 0 0 ║

║ 1 0 0 0 1 1 0 1 0 ║

║ 0 0 0 0 0 0 1 0 0 ║

A(G) = ║ 0 1 0 0 0 1 1 0 0 ║

║ 0 1 0 0 1 0 1 0 0 ║

║ 0 0 1 1 1 1 0 1 0 ║

║ 0 1 0 0 0 0 1 0 1 ║

║ 0 0 0 0 0 0 0 1 0 ║

Решение.

║ 0 1 0 0 0 0 0 0 0 ║

║ 1 0 0 0 1 1 0 1 0 ║

║ 0 0 0 0 0 0 1 0 0 ║

A(G) = ║ 0 1 0 0 0 1 1 0 0 ║

║ 0 1 0 0 1 0 1 0 0 ║

║ 0 0 1 1 1 1 0 1 0 ║

║ 0 1 0 0 0 0 1 0 1 ║

║ 0 0 0 0 0 0 0 1 0 ║

Изобразим граф G по матрице смежности.

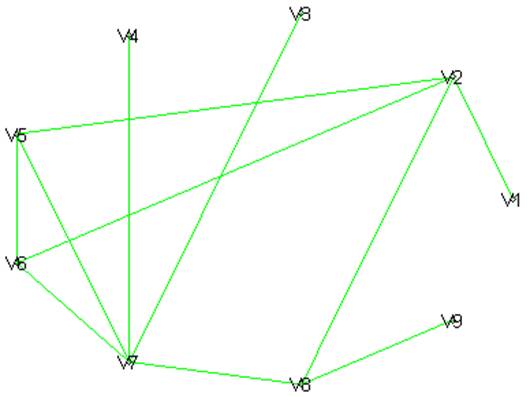
Составим таблицу степеней вершин, определяя по рисунку для

каждой из вершин количество выходящих из нее ребер

┌ ─ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┬ ─ ─ ─ ─ ┐

│ Vi │ v1 │ v2 │ v3 │ v4 │ v5 │ v6 │ v7 │ v8 │ v9 │

├ ─ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┼ ─ ─ ─ ─ ┤

│ S(Vi)│ 1 │ 4 │ 1 │ 1 │ 3 │ 3 │ 5 │ 3 │ 1 │

└ ─ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┴ ─ ─ ─ ─ ┘

В графе G будем обозначать ребро, соединяющее вершины

v и v, через a

i j ij

Матрица инцидентности для нашего графа имеет вид:

a a a a a a a a a a a

12 25 26 28 37 47 56 57 67 78 89

v1 ║ 1 0 0 0 0 0 0 0 0 0 0 ║

v2 ║ 1 1 1 1 0 0 0 0 0 0 0 ║

v3 ║ 0 0 0 0 1 0 0 0 0 0 0 ║

v4 ║ 0 0 0 0 0 1 0 0 0 0 0 ║

B(G) = v5 ║ 0 1 0 0 0 0 1 1 0 0 0 ║

v6 ║ 0 0 1 0 0 0 1 0 1 0 0 ║

v7 ║ 0 0 0 0 1 1 0 1 1 1 0 ║

v8 ║ 0 0 0 1 0 0 0 0 0 1 1 ║

v9 ║ 0 0 0 0 0 0 0 0 0 0 1 ║

Составим по рисунку таблицу расстояний и условных радиусов

┌ ─ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ┬ ─ ─ ─ ─ ─ ┐

│ │ v1 │ v2 │ v3 │ v4 │ v5 │ v6 │ v7 │ v8 │ v9 │ r(Vi)│

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v1 │ 0 │ 1 │ 4 │ 4 │ 2 │ 2 │ 3 │ 2 │ 3 │ 4 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v2 │ 1 │ 0 │ 3 │ 3 │ 1 │ 1 │ 2 │ 1 │ 2 │ 3 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v3 │ 4 │ 3 │ 0 │ 2 │ 2 │ 2 │ 1 │ 2 │ 3 │ 4 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v4 │ 4 │ 3 │ 2 │ 0 │ 2 │ 2 │ 1 │ 2 │ 3 │ 4 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v5 │ 2 │ 1 │ 2 │ 2 │ 0 │ 1 │ 1 │ 2 │ 3 │ 3 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v6 │ 2 │ 1 │ 2 │ 2 │ 1 │ 0 │ 1 │ 2 │ 3 │ 3 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v7 │ 3 │ 2 │ 1 │ 1 │ 1 │ 1 │ 0 │ 1 │ 2 │ 3 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v8 │ 2 │ 1 │ 2 │ 2 │ 2 │ 2 │ 1 │ 0 │ 1 │ 2 │

├ ─ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ┼ ─ ─ ─ ─ ─ ┤

│ v9 │ 3 │ 2 │ 3 │ 3 │ 3 │ 3 │ 2 │ 1 │ 0 │ 3 │

└ ─ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ┴ ─ ─ ─ ─ ─ ┘

Определим по таблице расстояний центр и радиус графа.

Радиус графа r(G)=2, следовательно, центр графа -

это множество вершин {v8}

Задача 4

Выяснить, применима ли машина Тьюринга T к слову P.

Если применима, то выписать результат T(P) применения

машины Тьюринга T к слову P.

┌

│ q1 1 q1 1 R

│ q1 0 q2 0 R

T: < q2 0 q2 0 L

│ q3 1 q3 0 R

│ q3 0 q3 0 L

└

P=11111001

Предполагается, что начальный момент Машина Тьюринга

обозревает самую левую единицу слова.

Решение. P=11111001

Согласно алгоритму функционирования машины Тьюринга имеем:

q1 11111001

1 q1 1111001

11 q1 111001

111 q1 11001

1111 q1 1001

11111 q1 001

111110 q2 01

11111 q2 001

1111 q2 1001

Машина Тьюринга применима к слову P и

T(P)=11111001.

Задача 5

Найти число способов расстановки 25 томов на

книжной полке, при котором первые 24 томов стоят

рядом в порядке возрастания номеров.

Решение.

В условиях задачи можно считать первые 24 томов одним

томом. Поэтому можно считать, что число разных томов 2.

Число способов расстановки равно числу перестановок P = 2! = 2

Задача 6

В военном подразделении служат 12 офицеров и 13 рядовых

оперативная группа состоит из командира, заместителя и 10 рядовых,

причём командир и заместитель назначаются случайным образом

из числа офицеров. Найти число возможных различных

оперативных групп.

Решение.

10 рядовых из имеющихся 13 рядовых можно выбрать

10 13!

C = ─ ─ ─ ─ ─ = 286

13 10! 3!

Командира и заместителя из имеющихся 12 офицеров можно

2 12!

выбрать A = ─ ─ ─ = 12∙ 11 = 132 способами,

12 10!

поскольку в данном случае пары являются упорядоченными (один

командир, а другой - заместитель или наоборот). Отсюда общее число

способов N = 37752

Задача 7

Найти множество всех подмножеств множества {4, 3, 6}

Решение.

Любое множество содержит пустое множество. Далее

последовательно добавляем одноэлементные подмножества

{4}, {3}, {6}, двухэлементные {4, 3}, {4, 6}, {3, 6},

трёхэлементное {4, 3, 6}.

Окончательно получим

{Ф, {4}, {3}, {6}, {4, 3}, {4, 6}, {3, 6}, {4, 3, 6}}

Задача 8

Найти декартово произведение множеств A={4, 1}, B={8, 7, 6}

12 Следующая ⇒