Контакты

Случайная статья

Задача № 7 з алгебри та геометрії

⇐ ПредыдущаяСтр 2 из 2

Задача № 7 з алгебри та геометрії

Знайти відстань від точки 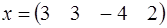до лінійного підпростору , що задається системою рівнянь:

.

.

~

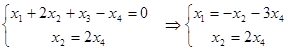
х₁х₂х₃х₄

-1 0 1 0

-3 2 0 1

Знайшли фундаментальну систему розв’язків

,

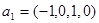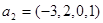
Розв’яжемо систему:

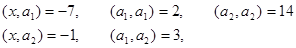
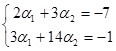
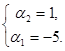
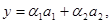де 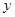- проекція вектор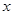а на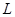

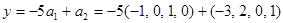
Нехай z – ортогональна складова, тоді

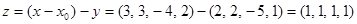
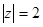
Задача № 8 з алгебри та геометрії

Знайти жорданову нормальну форму матриці .

Знайдемо власні числа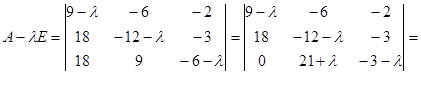

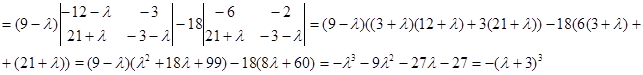Отже одержали, що існує власне число 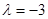кратності 3. Знайдемо кількість клітин Жордана 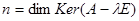, де 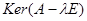- ядро 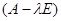складається з векторів х: 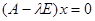. Знайдемо базис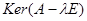

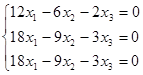
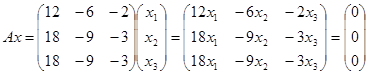
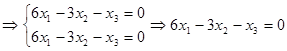
Фундаментальна система розв‘зків має вигляд:

х₁х₂х₃

1 0 6 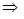Отримали два вектора (1, 0, 6) і (0, 1, -3).

0 1 -3

Отже матриця Жордана має 2 клітини. Так, як розмірність матриці А рівна 3, то клітини мають розмірність 1, 2, тобто

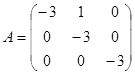
Задача № 9 з алгебри та геометрії

Знайти власні вектори та власні числа лінійного оператора, заданого в деякому базисі матрицею:

.

Розв‘язок:

~ ~

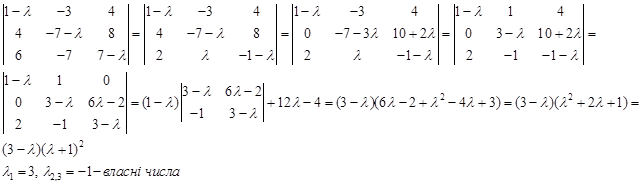
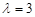
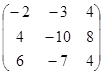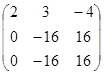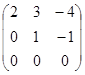
х₁х₂х₃

½ 1 1 а₁=(1, 2, 2)

~ ~

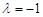
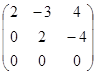х₁х₂х₃

1 2 1 а₂=(1, 2, 1)

Задача № 10 з алгебри та геометрії

Для даної матриці знайти обернену матрицю (порядок матриці дорівнює ):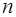

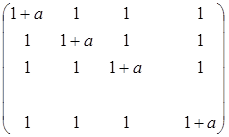
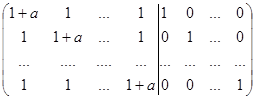
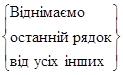
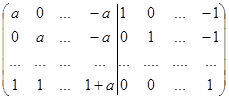
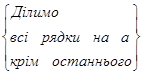
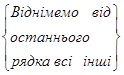
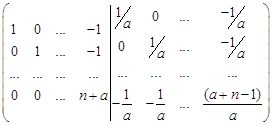
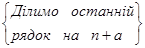
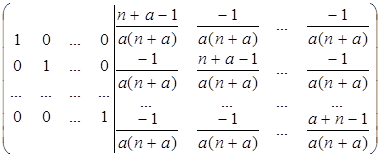
Отже

А^-1= 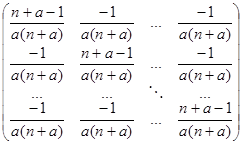або

⇐ Предыдущая 12

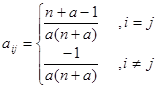
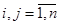
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.