Хелпикс

Главная

Контакты

Случайная статья



Задача № 1 з алгебри та геометрії

Стр 1 из 2Следующая ⇒


Задача № 1 з алгебри та геометрії

 

=

 

=

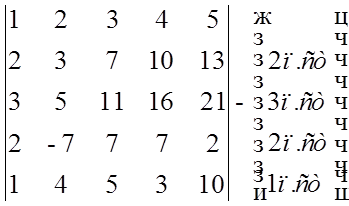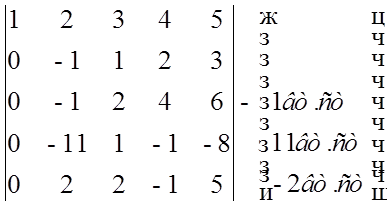1* =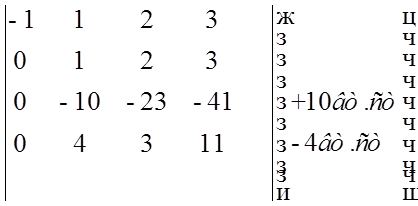

-1* 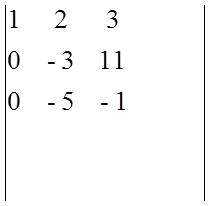=-1*(3-55)=-52

 

Задача № 2 з алгебри та геометрії

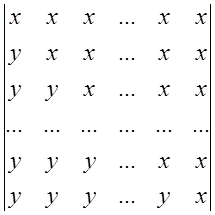
    От i отнимаем i-1 рядок                                            

 

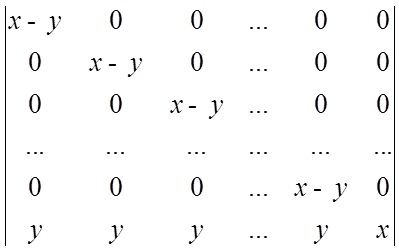
Трикутний визначник

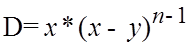
Задача № 3 з алгебри та геометрії

Скласти рівняння площини, що проходить через точку M1(2; 1; -1) паралельно векторам a1= {1; -1; 5}, a2= {2; 3; 7}.

Р-ня площини

  ,

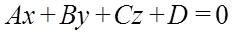якщо площина паралельна вектору а, то вектор нормалі на вектор а мають бути ортогональні, тобто скалярний добуток рівен нулю. підставляємо точку і маємо систему з 3 рівнянь.

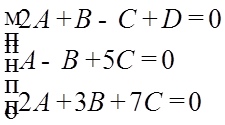
Наприклад  D=1, А=-11/31, В=-17/62, С=1/62

Відповідь:

 

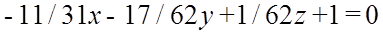
Задача № 4 з алгебри та геометрії

 

Скласти рівняння площини, що проходить через три точки M1(1; -1; 1), M2(0; 2; 4), M3(1; 3; 3).

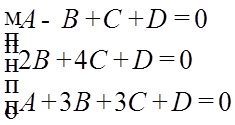
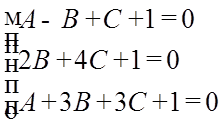
A=-1/2, B=1/6, C=-1/3;

Відповідь:

 

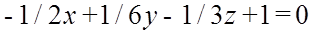
Задача № 5 з алгебри та геометрії

Скласти рівняння площини, що проходить через точки M1(1; 3; 1), M2(3; 0; 2) паралельно вектору

a = {2; 5; -2}.

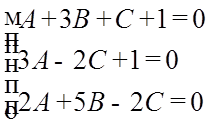
A=-21/31, B=2/31, C=-16/31;

Відповідь:

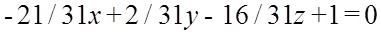
Задача № 6 з алгебри та геометрії

Дослідити сумісність, знайти загальний розв’язок і один частинний розв’язок СЛАР:

 

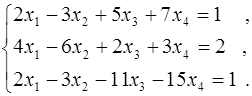
Для того щоб система була сумісна треба щоб ранг розширеної матриці 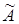 дорівнював рангу простої матриці .

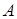Перетворимо (перетвореннями рядків які не змінюють рангу матриці) розширену матрицю:

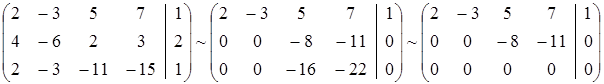
Отже 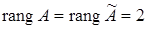 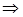система сумісна

т. я. матриця системи має ранг рівний двом то ми повинні дві змінні обрати параметрами. Нехай це будуть змінні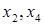

Тоді загальний розв’язок ,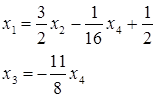

знайдемо якийсь частковий розв’язок. Нехай 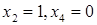, тоді ,

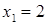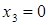
Отже частинний розв’язок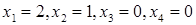


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.