Практическая часть

Сгенерируем массив значений в Mathcad, при этом укажем число измерений (N), математическое ожидание (m), СКО (sko).

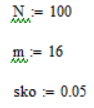
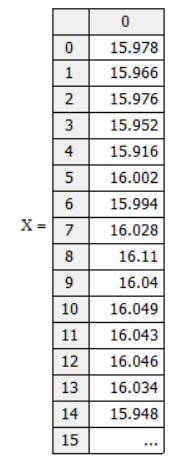
Для построения эмпирических кривых закона распределения случайных величин разобьем весь полученный диапазон результатов измерений на r интервалов.

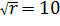
Импортируем данный массив в Microsoft Excel. И сортируем по возрастанию, после чего получаем x_min и x_max.

X_min = 15, 8549564037326; x_max = 16, 152407614932.

После рассчитаем дисперсию, СКО, асимметрию и эксцесс, используя данные таблицы 1.

Таблица 1 – Необходимые данные для расчета.

№	xi	xi-M_x	(xi-M_x)^2	(xi-M_x)^3	(xi-M_x)^4	Mx
	15, 8549564037326	-0, 13752	0, 018912	-0, 0026008	0, 000357664	15, 99248
	15, 8579803442158	-0, 1345	0, 018089	-0, 00243297	0, 000327228
	15, 892144984417	-0, 10033	0, 010067	-0, 00101	0, 000101336
	15, 8984393812873	-0, 09404	0, 008843	-0, 00083159	7, 8201Е-05
	15, 9157157620914	-0, 07676	0, 005892	-0, 00045231	3, 47196Е-05
	15, 9192587218869	0, 07322	0, 005361	-0, 00039252	2, 87399Е-05
	15, 9294401561516	0, 06304	0, 003974	-0, 00025049	1, 57902Е-05
	15, 9310961237625	0, 06138	0, 003768	-0, 00023126	1, 41952Е-05
…	…	…	…	…	…

1. Рассчитаем дисперсию по формуле (4), в нашем случае D(x) = 0. 0024112

2. Рассчитаем СКО по формуле (5), в нашем случае sko = 0. 049104

3. Рассчитаем коэффициент асимметрии по формуле (6), в нашем случае А = 0, 005202881

4. Рассчитаем эксцесс по формуле (7), в нашем случае Е = 0, 77316

5. Рассчитаем ошибки репрезентативности асимметрии и эксцесса по формулам (8) и (9), в нашем случае они равны m_A = 0. 244948974 и m_E = 0. 489897949

6. Сравниваем коэффициента асимметрии и эксцесс с ошибками их репрезентативности.

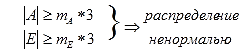
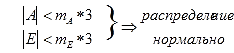
В нашем случаем распределено не нормально, так как коэффициент асимметрии больше, чем ошибка его репрезентативности, умноженная на 3.

7. Число интервалов мы уже определили, поэтому рассчитываем величину интервала, определяем число попаданий значений в полученные интервалы и построим гистограмму распределения результатов многократных измерений.

Таблица 2 – Частоты, попавшие в заданный интервал.

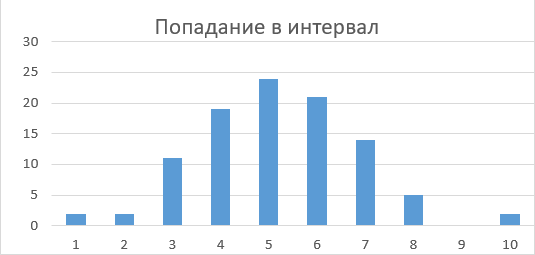
Рисунок 3 – Гистограмма распределения

После этого проделываем все тоже самое, только с измеренными значениями.

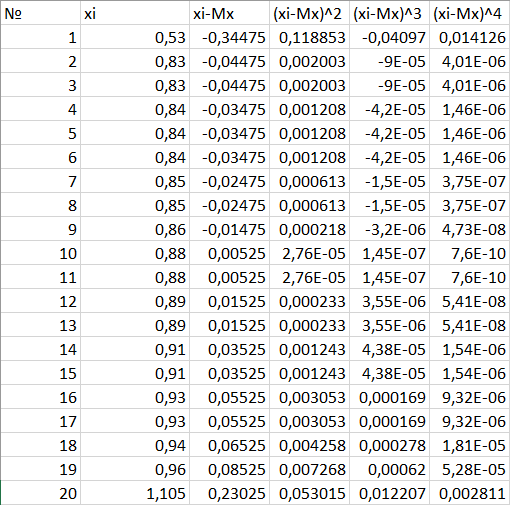
Рисунок 2 – Необходимые данные для расчета с измеренными значениями

1. Рассчитаем дисперсию по формуле (4), в нашем случае D(x) = 0. 010609091

2. Рассчитаем СКО по формуле (5), в нашем случае sko = 0. 103001

3. Рассчитаем коэффициент асимметрии по формуле (6), в нашем случае А = -1, 2709545

4. Рассчитаем эксцесс по формуле (7), в нашем случае Е = 4, 570813

5. Рассчитаем ошибки репрезентативности асимметрии и эксцесса по формулам (8) и (9), в нашем случае они равны m_A = 0. 547722558 и m_E = 1, 095445115

6. Сравниваем коэффициента асимметрии и эксцесс с ошибками их репрезентативности.

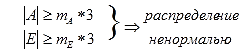
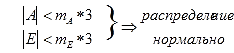
В нашем случаем распределено не нормально, так как эксцесс больше, чем ошибка его репрезентативности, умноженная на 3.

Таблица 3 – Частоты измеренных значений, попавшие в интервал.

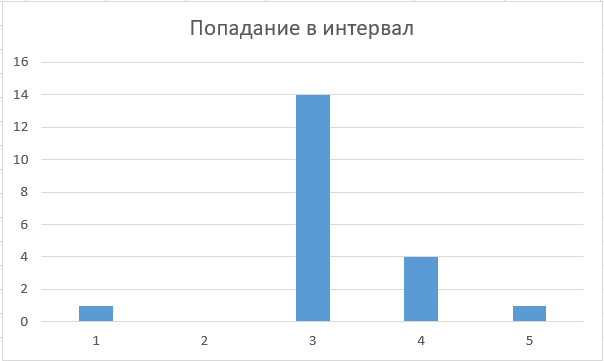
Рисунок 3 – Гистограмма распределения измеренных значений

Вывод

В данной лабораторной работе мы получили навыки проведения измерений на базе аналогового вольтметра с последующей обработкой полученных данных и анализом эмпирического закона распределения результатов многократных измерений.

⇐ Предыдущая 12