Задание на лабораторную работу

Стр 1 из 2Следующая ⇒

Министерство науки и высшего образования Российской Федерации

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Алтайский государственный технический университет

им. И. И. Ползунова»

Факультет (институт) ___________________________________

Кафедра ______________________________________________

наименование кафедры

Отчет защищен с оценкой________

Преподаватель _________________

(подпись) (и. о. фамилия)

“____”___________ 20___ г.

Отчет

по лабораторной работе № 1

Определение статистических характеристик закона распределения результатов многократных измерений

по дисциплине

____________________" Метрология" ________________

наименование дисциплины

ЛР 12. 03. 01. №. 0012 О

обозначение документа

Студент группы _____________________________________________

и. о., фамилия

Преподаватель _____________________________________________

должность, ученое звание и. о., фамилия

БАРНАУЛ 2020

Задание на лабораторную работу

Тема: Определение статистических характеристик закона распределения результатов многократных измерений

Цель работы: получение навыков проведения измерений на базе аналогового вольтметра с последующей обработкой полученных данных и анализом эмпирического закона распределения результатов многократных измерений.

Лабораторное задание:

1 произвести измерения заданных преподавателем параметров с использованием аналогового вольтметра (вольтметр В7–16 ).

2 получить выборку чисел в программе MathCad.

3 осуществить статистическую обработку результатов многократных наблюдений, в результате чего определить параметры закона распределения случайных величин.

4 повторить пункт 3 для измеренных значений.

Задание принял к исполнению _ _ студент гр. ПС-92 В. В. Крафт

(подпись)

Теоретические сведения

Центральные моменты.

Особое значение для характеристики распределения случайной величины имеют числовые характеристики, называемые начальными и центральными моментами.

Начальным моментом k-го порядка α _k(Х) случайной величины Х называется математическое ожидание k-ой степени этой величины, т. е.

α _k(Х) =М(Х^k) (1)

Математическое ожидание – является начальным моментом первого порядка, или, как говорят, первым начальным моментом:

М(Х) =α ₁(Х). (2)

Центральным моментом k-го порядка μ _k(Х) случайной величины Х называется математическое ожидание k-ой степени центрированной случайной величины, т. е.

μ _k(Х) = М[(Х – М(Х))^k] (3)

Иначе говоря, центральный момент k-го порядка – это математическое ожидание k-ой степени отклонения.

Очевидно, что центральный момент первого порядка равен нулю, так как это ни что иное, как математическое ожидание отклонения, которое равно нулю.

Итак, моменты первого и второго порядков (математическое ожидание и дисперсия) характеризуют самые важные черты распределения: его положение и степень разброса значений.

Дисперсия- (от лат. dispersio - рассеяние), в математической статистике наиболее употребительная мера рассеивания, отклонения случайных значений от среднего. Если дисперсия имеет большое числовое значение, то данная случайная величина имеет большой разброс значений и соответствующая кривая распределения имеет более пологий вид, чем кривая, для которой второй центральный момент имеет меньшее значение. Поэтому второй центральный момент характеризует, в какой-то степени, " плосковершинность" или " островершинность" кривой распределения. Однако эта характеристика не очень удобная. Центральный момент второго порядка имеет размерность равную квадрату размерности случайной величины.

Для выборочной совокупности дисперсия рассчитывается по следующей формуле:

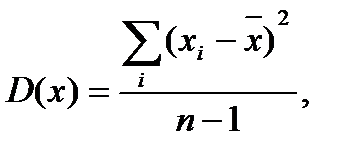(4)

где n - число измерений, x_i - единичное значение, 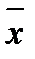- среднее арифметическое значение выборки.

Среднеквадратическое отклонение определяется как квадратный корень из дисперсии случайной величины:

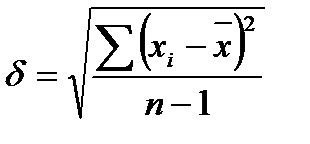(5)

Коэффициентом асимметрии А_s или просто асимметрией называется отношение центрального момента третьего порядка к кубу среднеквадратического отклонения, т. е

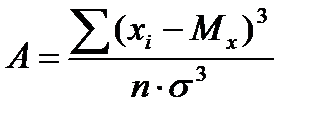(6)

Асимметрия – это показатель симметричности/скошенности кривой распределения, а эксцесс определяет ее островершинность.

При левосторонней асимметрии ее показатель является положительным и в распределении преобладают более низкие значения признака. При правостронней – показатель положительный и преобладают более высокие значения. У всех симметричных распределений (в том числе, и у нормального распределения) величина асимметрии равна нулю.

Рисунок 1 – Асимметрия

Эксцессом E_k называется величина, определяемая по формуле:

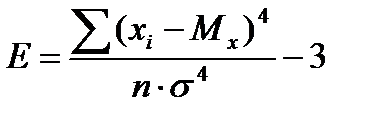(7)

Эксцесс, в основном, применяется для непрерывных случайных величин и служит для характеристики, так называемой " крутости" кривой распределения, или иначе, как уже было сказано, для характеристики " плосковершинности" или " островершинности" кривой распределения. В качестве эталонной кривой распределения считается кривая нормального распределения. Для случайной величины, распределенной по нормальному закону, имеет место равенство 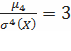. Поэтому эксцесс, заданный формулой (7), служит для сравнения данного распределения с нормальным, у которого эксцесс получается равным нулю.

Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения 2 вершины (бимодальное распределение), то тогда эксцесс стремится к отрицательной величине.

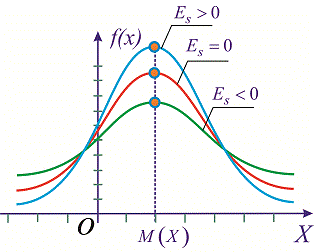
Рисунок 2 – Эксцесс

Распределение оценивается как предположительно близкое к нормальному, если установлено, что от 50 до 80 % всех значений располагаются в пределах одного стандартного отклонения от среднего арифметического, и коэффициент эксцесса по абсолютной величине не превышает значения равного двум.

Необходимо также определение ошибок репрезентативности асимметрии и эксцесса:

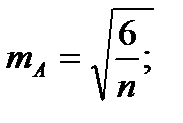(8)

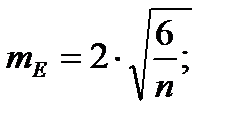
(9)

Распределение считается достоверно нормальным если абсолютная величина показателей асимметрии и эксцесса меньше их ошибок репрезентативности в 3 и более раз.

Как уже было сказано выше, принцип определения нормальности-ненормальности распределения является следующим:

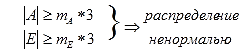
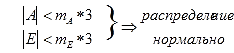
Если оба показателя не превышают в 3 раза свою собственную ошибку репрезентативности, можно заключить, что распределение результатов многократных измерений соответствует нормальному.

12 Следующая ⇒