
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЭТ-19 Математика 11.05.20
ЭТ-19 Математика 11. 05. 20
Тема: Решение прикладных задач с помощью определенного интеграла
Задание:
- Посмотрите видео ролик № 1: https: //youtu. be/53Y2FYsf6xI
- Запишите в тетрадь ниже приведенный опорный конспект.
- Посмотрите видео ролик № 2: https: //youtu. be/7hhrgW7OR2w , запишите в тетрадь примеры решения заданий.
- Решить задачи для самостоятельного решения.
- Отчет по работе отправить до конца дня по ссылке:
https: //vk. com/topic-193913663_41525223
Опорный конспект
по теме «Решение прикладных задач с помощью определенного интеграла»
1. Задача о вычислении пути
Пример 1. Скорость прямолинейного движения тела выражается формулой u = 2t+3t  (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
S=  u(t)dt, (1)
u(t)dt, (1)
Решение.
1. t  =0с; t
=0с; t  = 5с.
= 5с.
2. По формуле (1) найдем путь, пройденный телом за 5 сек.
S=  2t+3t
2t+3t 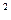 )dt = (t
)dt = (t  )
)  = (52 + 53) – (02 + 03) = 25 + 125 – 0 = 150(м).
= (52 + 53) – (02 + 03) = 25 + 125 – 0 = 150(м).
Ответ. S=150 м.
Пример 2. Скорость движения тела задана уравнением u = 15t – 3t 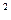 (м/с). Определить путь, пройденный телом от начала движения до остановки.
(м/с). Определить путь, пройденный телом от начала движения до остановки.
Решение.
1) В момент начала движения и в момент остановки у тела скорость u = 0. Найдем значение времени в эти моменты. Для этого решим уравнение u = 0.
15t – 3t 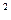 = 0
= 0
3t(5 – t) = 0
t = 0 или t = 5
S =  15t – 3 t
15t – 3 t 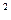 )dt =
)dt = 
 =
= 
 =
=

Ответ: S = 62, 5 м.
Пример 3. Скорость движения тела изменяется по закону u = 2t (м/с). Найти длину пути, пройденного телом за третью секунду его движения.
Решение:
Формулу используем эту же S=  u(t)dt,
u(t)dt,
Только нам надо правильно определить t1 и t2.
t1 будем считать началом третьей секунды, а t2 – концом этой секунды. Итак, третья секунда длится от конца 2-ой до конца 3-ей секунды.
Значит t1 = 2 и t2 = 3.
Вычисляем интеграл S = 
Ответ: S = 5 м.
2. Задача о вычислении работы переменной силы.
Работа A этой силы F вычисляется по формуле:
А=F*s, (2)
Где S – перемещение, м.
Если F – сила упругости, то по закону Гука
F=kx, (2*)
где x- величина растяжения или сжатия,
k – коэффициент пропорциональности.
Работа переменной силы вычисляется по формуле (4)
A= 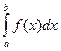 (3)
(3)
Пример 4. Сила упругости F пружины, растянутой на 1  =0, 05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1
=0, 05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1  = 0, 1м?
= 0, 1м?
Решение
1. Определим коэффициент пропорциональности k.
Подставим формулу (2*) F=3 H, x = 0, 05 м:
3=k*0, 05, т. е. k=60, следовательно, F=60x=f(x).
2. Подставив F=60x в формулу (3), найдем значение работы переменной силы, полагая, что а=0; b=0, 1:
A= 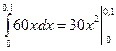 =0, 3Дж
=0, 3Дж
Ответ. А = 0, 3Дж.
3. Задача о силе давления жидкости.
Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле
P=gphS, (4)
Где g – ускорение свободного падения в м/с 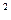 ;
;
p – плотность жидкости в кг/м 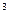 ;
;
h– глубина погружения площадки в м;
S – площадь площадки в м 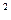 ;
;
Сила давления жидкости на вертикальную пластину вычисляется по формуле (5)
P=g 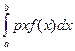 . (5)
. (5)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|