Задача 9

Задача 9

Определить гибкость элемента по формуле:

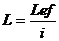, где ,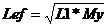

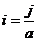
i - радиус инерции поперечного сечения;

L1=1000 см - длина элемента;

My=0. 7 - коэффициент, зависящий от способа закрепления концов стержня;

j=2000 см⁴- момент инерции поперечного сечения стержня;

a=96 см² - площадь поперечного сечения стержня.

Задача 10

Определить приведенную гибкость составного стержня сквозного сечения с планками по формуле:

, где

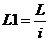- гибкость отдельной ветви;

L=78 см - длина ветви;

i=2. 1 см - радиус инерции сечения отдельной ветви;

Ly=50 - гибкость ветви относительно оси Y;

n=1. 2 - коэффициент, зависящий от соотношения жесткостей и размеров ветвей и планок.

Задача 11

Определить расчетную длину стержня с различными сжимающими усилиями по длине стержня, используя формулу:

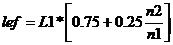, где n1 > n2.

L1=600 см - длина стержня;

n1=70 - усилие на первом участке стержня;

n2=30 - усилие на втором участке стержня.

Задача 12

Определить значение коэффициента продольного изгиба по формуле:

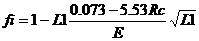, где , ,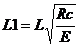

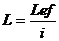L1 - условная гибкость;

Rc=2400 кгс/см² - расчетное сопротивление;

E=2. 1E6 кгс/см² - модуль упругости;

Lef=1000 см - расчетная длина элемента;

i=5 см - радиус инерции поперечного сечения элемента

Задача 13

Определить значение коэффициента продольного изгиба по формуле:

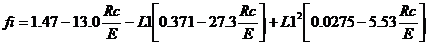где L1 - условная гибкость, равная

, ,

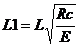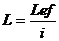Rс=2400 кгс/см² - расчетное сопротивление;

E=2. 1E6 кгс/см² - модуль упругости;

Lef=1000см - расчетная длина элемента;

i=12 см - радиус инерции поперечного сечения элемента.