Хелпикс

Главная

Контакты

Случайная статья



Министерство РФ науки и образования

Стр 1 из 2Следующая ⇒


Министерство РФ науки и образования

Московский Государственный Открытый Университет

Губкинский институт (филиал МГОУ)

 

 

Курсовая работа

по “Теоретическим основам

электротехники”

 

                                                                    

 

 

                                                                      Выполнил:

                                       Студент 3 курса

                                             горного факультета

                                                                      Матюхин Алексей Иванович

                                    Шифр: 802500

                                                   Специальность: 100400

                             Проверил:       

                                                                    Богданов Виктор Михайлович                                                                          

 

 

                                                                 Губкин

2005
Определение варианта к индивидуальному заданию.

        

А Б В Г Д Е
А Б Д Е В Г
a b c d e f

 

Последняя цифра
А
Б

 

 

a b c d e F

Рассчитанный код:  

Задание №1

 

В схеме каждая ветвь содержит E и R, а одна ветвь только источник тока.

1. 1  

Ecd=E(5-c)*(5-e)=E34=E24=50 B

E(5-c)*(5-f)= E(5-f)*(5-d)= E(5-d)*(5-e)= E23=E31=E14=30 В

Eef=E12-?

1. 2

Jab= J12= 0, 9 А

1. 3

Rcd=Rdf=Rdc=R34=R42=R41=80 Ом

Rce=Rcf=Ref=R31=R32=R12=40 Ом

1. 4

Ief= I12= 0, 6 А

 

Задание:

1. Начертить схему в соответствии с исходными данными, соединяя зажимы ветвей прономерованных одинаково в один узел.

2. Произвести анализ схемы, определить число независимых уравнений Кирхгофа. Составить и решить систему из этих уравнений.

3. Определить неизвестные токи и ЭДС, применив метод контурных токов.

4. Составить уравнение баланса мощностей и посчитать.

5. Считая известными все ЭДС и ток источника тока. Составить систему уравнений для определения тока в элементе Rcd=R34, I24, применив метод эквивалентного генератора. Попутно использовать методы узловых потенциалов и эквивалентных преобразований, соединенных резистивных элементов.

Решение.

1. Начертим схему согласно исходным данным.   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


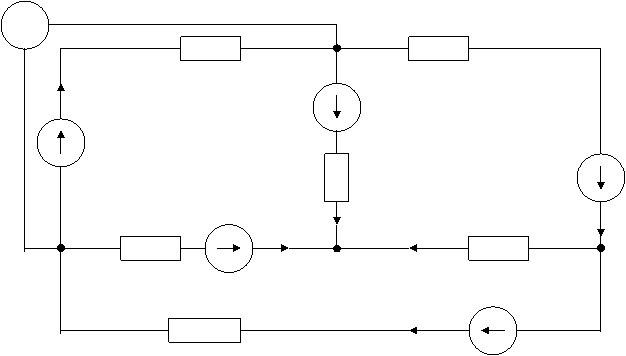
2. Составим 3 уравнения по I закону Кирхгофа:


 

Составляем контурные уравнения по II закону Кирхгофа:

(в-вит)-(y-1)=(7-1)-(4-1)=6-3=3 (уравнения):


 

                                  

 

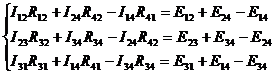
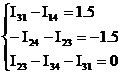
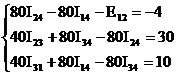
I31 =x1                              I23=x4

I14 =x2                                                  I34=x5

I24 =x3                            E12=x6

 

 

X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
.
.
-
=
+
=
-
+
-
=
-
+
-
=
-
-
+
+
=
+
-
=
ì
í
ï
ï
ï
ï
î
ï
ï
ï
ï


                                   

 

                   

 

Решая, систему уравнений в Math cad получим:

 

 

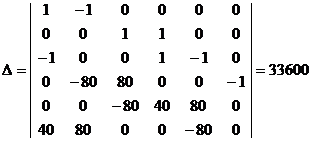
Δ 1=38000 Δ 2=-12400 Δ 3=10000 Δ 4=40400 Δ 5=24000 Δ 6=1926000

 

I31= 1. 131 A                             I34= 0, 071 A     

I23= 1. 202 A                             I24= 0. 298 A

I14= -0. 369 A                            E12= 57. 321 B

 

3. Определим неизвестные токи, применив метод контурных токов:

Составляем систему уравнений:

 

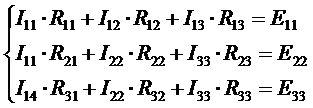
Контурные ЭДС:

E12э=E12+ J12*R12

   E11= E12+E24-E14=E12+J12*R12+E24-E14=E12+56

E22= E23+E34-E24=30

E33= E14-E34+E31=10

 

  Токи:

I12= 0, 6 A J12=0. 9 I11=J12+I12=1. 5

 

Собственные сопротивления контуров:

R11=R12+R42+R41=40+80+80=200 Ом

R22=R32+R34+R42=40+80+80=200 Ом

R33=R41+R34+R31=80+80+40=200 Ом

R12=R21=-R42=-80 Ом

R13=R31=-R41=-80 Ом

R23=R32=-R34=-80 Ом

 

Подставим значения в систему:

 


 

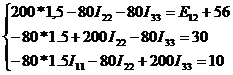
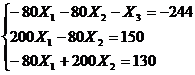
Решая, систему уравнений в Math cad получим:

I22 = x1 = 1. 202               I33= x2 =1. 131                 E12= x3 =57. 33

 

 

  Определим неизвестные токи:

I22=I23=1. 202 A

I33=I31=1. 131 A

I14= I33- I11= -0. 369A

I24= I11-I22=0. 298 A

I34= I22-I33 = 0. 071 A

E12=57. 33 B

 

 

4. Составим уравнение баланса мощности:

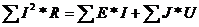
I12 =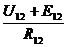

 

 

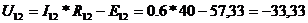
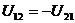
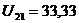
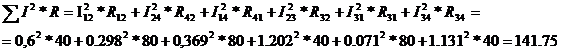
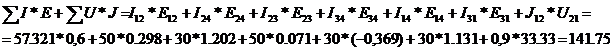
141. 75=141. 75

 

 

5. Рассчитаем j1, j2, j3 методом узловых потенциалов:

Заземляем 4 узел, т. е. j4=0.

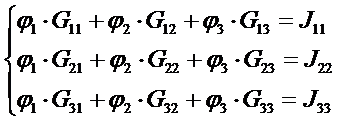
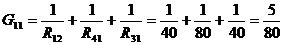 см

 см

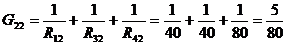 см

 

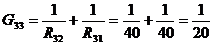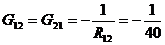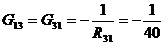см

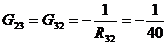см

см

 

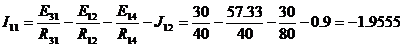 A

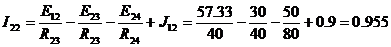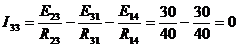 А

А 

 

 

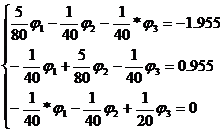
Решая, систему уравнений в Math cad получим:

 

φ 1= -56, 628 В            φ 2= -23. 368 В     φ 3= -40. 007 В

 

 

Используя метод эквивалентных преобразований резистивных элементов

определяем входное сопротивление Rвх:

 

 

     
 

 

 


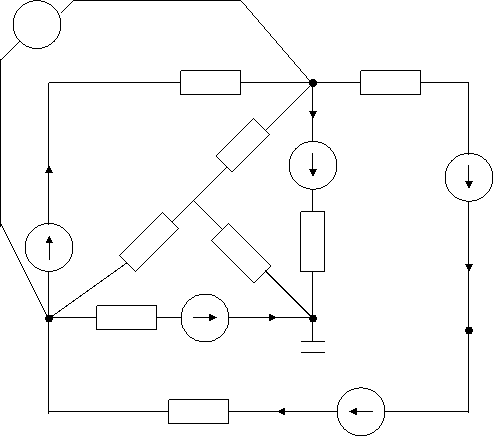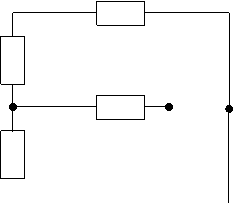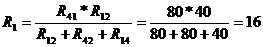Ом

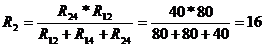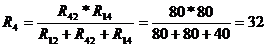Ом

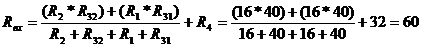Ом

 

 Ом

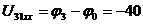В

 

Определяем ток в элементе R12, применив метод эквивалентного генератора.

 

A

 

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.