- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
3.Вопрос. 4.Вопрос. 5.Вопрос. Алгебра тензоров
3. Вопрос
Опр. Упорядоченная совокупность базисных векторов называется их индефинитным произведением или полиадой. Количество векторов в полиаде- её ранг.
1)Две полиады равны тогда и только тогда, когда они состоят из одних и тех же векторов в одном и том же порядке. R1R2R3= R1R2R3
2)умножение на скаляр. α (R1R2 )= (α R1)R2 = R1 (α R2)
3)для полиад одного ранга вводится сложение(коммутативность, ассоциативность). R1R2 +R3R2 =R3R2 +R1R2
4)сумма произведений полиад одного ранга на скаляры называется их линейной комбинацией. α (R1R2)+β (R3R2 )
5)совокупность полиад одного ранга называется линейно-независимой, если ни одна из них не может быть представлена линейной комбинацией остальных.
RiRj =( R1 R1 , R1R2 , R1R3 , … R3R3 )
Для полиад вводятся операции умножения:
1)скалярное умножение RiRjRl ∙ RmRnRk (Rl ∙ Rm ) RiRjRnRk 2)векторное произведение RiRj (Rk * Rm ) RnRl
3)индефинитное умножение. при индеф. умножении сначала выписываем все в-ры 1-го множителя и к ним присоединяем в-ры 2-го. RiRj; RnRk RiRjRnRk
второе определение тензора: тензором ранга n назыв. объект U независящий от системыкоординат, который в каждойконкретной системе координат представляется линейной комбинацией всевозможных полиад ранга n различной структуры U =UijkRiRjRk=UijkRiRjRk=…=UijkRiRjRk коэффициенты разложения называются координатами тензора ковариантными по нижним индексам и контравариантными по верхним. Так же как и в опр. вектора, опр. 1 и 2 тензора являются эквивалентными
4. Вопрос
Матричный тензор
| glj=Ri∙ Ri gij=Ri∙ Rj δ iJ=Ri∙ Rj gi’j’=Ri’∙ Rj’ gi’j’=Ri’∙ Rj’ δ j’i’=Ri’∙ Rj’ | 1)Ri=ajiRi=(по осн. Теор. Бизиса) │ ∙ Rk =aj1∙ R1+aj2R2+aj3R3 Ri∙ Rk=gik=aji∙ Ri∙ Rk=aji∙ δ jk=ajk Rj=gji∙ Rj(5) 2)Ri=bikRk │ ∙ Rj Ri=gikRk (5) RiRj=gij=bik δ kj=bji |
Операция опускания и поднятия индексов (5)
Рассм. Выраж: Rj∙ Rj=δ ji=gin∙ Rn∙ gikRk=gjn∙ gikδ nk=gingin= (сво-во: gji=gij, gij=gji)) =gjn∙ gni=δ ji => gin∙ gni=δ ji
ð ||gin||=||gnj||-1
Вычисляем определитель M: |gin|∙ |gni|=1
|gnj|=g, |gni|=g-1
Рассм: gi’j’=Ri’∙ Rj’= выразим по формулам = 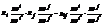 ;
;
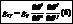
G=gijRi∙ Rj= (C использ. (5) )= gij∙ gikRkRj=δ kjRkRj=δ k∙ Rk∙ gjiRi=gKi∙ RkRi
g-коорд. Метрическ. Тензора.
ui=gikuk ui=gikuk sij=gimgjn∙ Smn
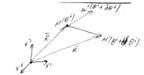
| рассмотрим. Т. M (над М знак вектора) MM’=R(M’)R(M)= =R(θ i+∂ θ i)R(θ i)= |
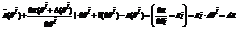

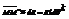
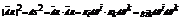
Если задана кривая 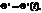 i=1, 2, 3.
i=1, 2, 3.
ds= 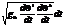 ;
; 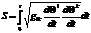 - длина дуги в кривол. коорд.
- длина дуги в кривол. коорд.
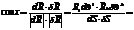
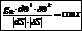
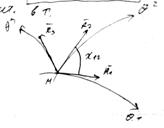
Рассмотрим элементы которые являются касат. в точке
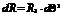
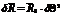
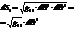
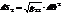
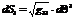
| 
|
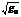 - явл. массштабн. множителем между приращ. крив. корд.
- явл. массштабн. множителем между приращ. крив. корд. 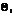 и длинами дуг соответств. коорд. линий
и длинами дуг соответств. коорд. линий
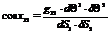
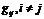 геом. смысл состоит в том, что эти парам. опред. углы между соотв. коорд. направлениями.
геом. смысл состоит в том, что эти парам. опред. углы между соотв. коорд. направлениями.
5. Вопрос
В каждой СК построим также числа Эijk=Ri(Rj·Rk), убедимся что такие числа являются координатами трехвалентного тензора.
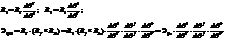
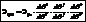 по первому определению тензора эти числа являются тензором ранга n. Эти числа Эijk являются компонентами трехвалентного тензора, который называют дискриминантным.
по первому определению тензора эти числа являются тензором ранга n. Эти числа Эijk являются компонентами трехвалентного тензора, который называют дискриминантным.
Операция поднятия индексов.
ginЭijk=Эnij=gin Ri (Rj·Rk)= Rn (Rj·Rk);
gingjmgklЭijk=Эnml=Rn(Rm·Rl)
Значение компонентов дискриминантного тензора.
1) При круговой перестановке значение не меняется
2) При транспозиции двух векторов знак меняется.
Эijk= -Эijk
Если среди трех индексов ijk имеются 2 одинаковых, то соответ. коорд. Обращается в 0. Среди 27 чисел ijk существенно отлично от нуля лишь одно, остальные находятся 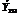 .
.
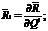
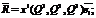
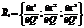
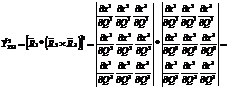 при транспонировании определитель не меняется.
при транспонировании определитель не меняется. 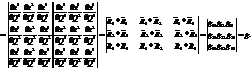
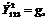
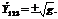
Чтобы выбрать знак, полагаем, что 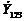 -положительное и равно
-положительное и равно 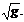
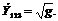
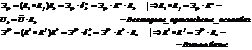
6 . Вопрос
Алгебра тензоров
С помощью алгебр. операций получаются новые тензоры
1)Тензоры одного ранга можно складывать.
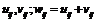 -тензор. Док-во:
-тензор. Док-во: 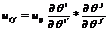
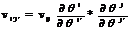 ;
;

2)Умножение тензора на скаляр. 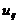 - тензор, то
- тензор, то 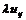 - тензор. Док-во:
- тензор. Док-во: 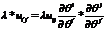 - преобраз. по тензорному закону, => тоже тензор.
- преобраз. по тензорному закону, => тоже тензор.
3)Свертывание тензора: Пусть заданы смешанные компоненты какого-либо тензора. Выберем один верхн. один нижний и придадим одинаковое значение. 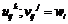
компонен. тензора.
Док-во: 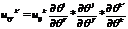
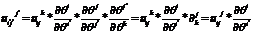
4) 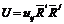 ,
, 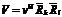
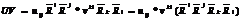
-скалярное 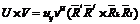 -векторное
-векторное
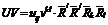 -- индефинитное
-- индефинитное
5)Операция симметр. и альтернации. Пусть задан тензор n-ого ранга. 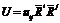 . Выпишем его корд. и составим n! возможных корд., кот. отвечают возможным перестановкам и построим.
. Выпишем его корд. и составим n! возможных корд., кот. отвечают возможным перестановкам и построим. 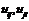 .
.
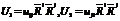 . Построим тензор, корд. кот. равны среднему аррифмет. выше построенным различным коорд-там.
. Построим тензор, корд. кот. равны среднему аррифмет. выше построенным различным коорд-там.
 -постр. тензор наз. построенным по средствам симметрирования.
-постр. тензор наз. построенным по средствам симметрирования. 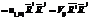
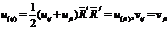 Построим тензор w=1/n! (сумма тенз. постр. выше)
Построим тензор w=1/n! (сумма тенз. постр. выше) 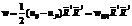
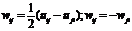 - тензор получ. из заданного посредством альтернации. Такой тензор назыв. кососимметр.
- тензор получ. из заданного посредством альтернации. Такой тензор назыв. кососимметр.
7. Вопрос
Простейшие св-ва
1) Если в какой-либо СК все компоненты т. Обратились к нулю, то они равны 0 во всех других СК 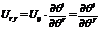
2) Пусть даны две тензоры. 1-ый симметричный, 2=ой кососимметричный
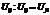
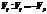
Тогда свёртка этих тензоров по ij обратится в 0
Д-во
Uij=Vij=0, Vij=0, Vij=-Vji.
V11=V22=V33=0
U12V12+U21V21+U13V13+U31V31+U23V23+U32V32=0
3) Обратный тензорный признак
Пусть в каждой СК заданы совокупности чисел снабженными индексами, обладающими св-ом, при свертке с любым тензором они образуют тензор, тогда заданные совокупности чисел являются коофициентами тензора.
Докажем на тензоре 2ого ранга, пусть в каждом СК заданы совокупности чисел с индексами I и j Uij при свертке получится Uijbj=Vi – тензор, где bi – любой
Т. к Ui – тензор => 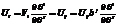 ,
,
а Vi’ тоже самое только в штрихованной системе 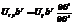 компоненты
компоненты  . Подставим
. Подставим 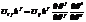 , переместим всё влево
, переместим всё влево 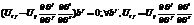
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|