
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Следовательно, что любое чётное числоначиная с 10, можно представить в виде суммы двух членов, из групп чиселOp.
⇐ ПредыдущаяСтр 2 из 2
Пример: Рассмотрим вариант:
A) N=10
10 не делится нацело на 6. Следовательно, сумма двух членовгруппы (Op), также не делиться нацело на 6.
Тогда, добавляем к 10 двойку,
Nизм. =10+2 =12
B) Найдем, все возможные члены группы чисел (Op)
T=( Nизм. /6)-1
Делим Nизм. на 6, чтобы исключить все варианты сложений, не связанных с группой (Op), вычитаем единицу поскольку число 1, мы не принимаем как, простое.
T – количество пар, членовгруппы чисел (Op).
T = 12/6 -1 = 1
Мы получили одну пару. (T=1)
D) Восстановим значения членов группы чисел (Op). Для это возьмём натуральный ряд и ограничим его T. ( 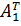 )
)
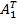 =1; 2; 3; …KT;
=1; 2; 3; …KT;
Где каждый член ряда, обозначается K.
Подставим полученные значения, в исходные формулы.
Op = 6*( 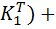 1 V6*(
1 V6*( 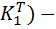 1
1
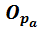 = 6*K1
= 6*K1 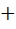 1
1
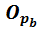 = 6*K1
= 6*K1 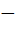 1
1
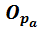 = 6*1
= 6*1 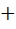 1 = 7
1 = 7
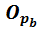 = 6*1 – 1 = 5
= 6*1 – 1 = 5
Поскольку N делится нацело на 6, лишь с добавлением двойки, делаем вывод, что N–сумма двух одинаковых членов группы чисел (Op), которые в свою очередь делятся на 6, лишь с вычетом двойки. (табл, 2. )
Т. е. для N=10, верно,  , в нашем случае равная пяти (5).
, в нашем случае равная пяти (5).
4. ) Докажем, что в группе чисел (Op), которая в виде суммы двухчленов, даёт любое чётное число, начиная с 10, есть хотя-бы, одна пара простых чисел, которая в сумме, даёт любое чётное число, начиная с 10.
A) Заметим, что с увеличением значений N, растёт T – количество пар, членов группы чисел (Op), следовательно, и сумм двух членов группы чисел (Op).
T = (Nизм. /6)-1
Рассмотрим несколько значений N.
N=12, 34, 74 …
Для N=12,
N=12 – без остатка делиться на 6, т. е. сумма двухчленовгруппы
( 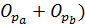 , также делиться нацелона 6, без дополнительных манипуляций.
, также делиться нацелона 6, без дополнительных манипуляций.
T = 12/6 -1 = 1
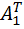 = 1; 2; 3; …KT;
= 1; 2; 3; …KT;
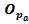 = 6*K1
= 6*K1 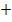 1
1
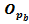 = 6*K1
= 6*K1 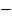 1
1
| K | 
| 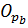
|
N=12=
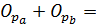 7+5
7+5
Для N=34,
N=34 – делиться на 6, лишь с добавлением двойки, т. е. сумма двухчленовгруппы
( 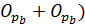 , также делиться нацелона 6, с вычетом двойки.
, также делиться нацелона 6, с вычетом двойки.
T = 36/6 -1 = 5
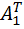 = 1; 2; 3; …KT;
= 1; 2; 3; …KT;
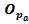 = 6*(1…5)
= 6*(1…5)  1
1
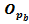 = 6*(1…5)
= 6*(1…5) 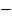 1
1
| K | 
| 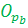
|
N=34=
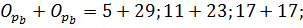
Для N=74,
N=74 – делиться на 6, лишь с вычетом двойки, т. е. сумма двухчленовгруппы ( 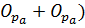 , также делиться нацелона 6, с добавлением двойки.
, также делиться нацелона 6, с добавлением двойки.
T = 72/6 -1 = 11
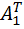 = 1; 2; 3; …KT;
= 1; 2; 3; …KT;
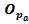 = 6*(1…11)
= 6*(1…11) 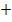 1
1
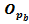 = 6*(1…11)
= 6*(1…11) 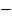 1
1
| K | 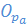
| 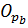
|
N=74 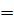
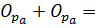 67+7; 61+13; 55+19; 49+25; 43+31; 37+37;
67+7; 61+13; 55+19; 49+25; 43+31; 37+37;
Из формулы распределения простых чисел, выведем частный случай, для членовгруппы чисел (Op), в которых по определению отсутствуют числа кратные 3 и 2.
π ( 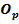 )= 6*
)= 6* 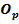 /ln(
/ln( 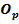 )
)
Вероятность того что, оба выбранныхчленов группы чисел (Op), окажутся простыми.
Для N делающейся на 6, лишь с вычетом двойки, верна следующаяформула:
 *
* 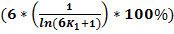 *
* 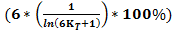 ;
;
Для N делающейся на 6, без дополнительных манипуляций, верна следующая формула:
 *
* 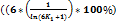 *
* 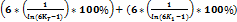 *
* 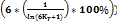 ;
;
Для N делающейся на 6, лишь с вычетом двойки, верна следующая формула:
 *
* 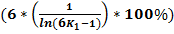 *
* 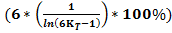 ;
;
Поскольку вероятность того что, выбранные два членов группы чисел (Op), окажутся простыми, достигает 100%, делаем вывод, что
в группе чисел (Op), которая в виде суммы двухчленов, даёт любое чётное число, начиная с 10, есть хотя-бы, одна пара простых чисел, которая в сумме, даёт любое чётное число, начиная с 10.
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|