- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Pa+Pb=NN>4
Проблема Гольдбаха (гипотеза Гольдбаха, проблема Эйлера, бинарная проблема Гольдбаха) — утверждение о том, что любое чётное число, начиная с 4, можно представить в виде суммы двух простых чисел.
Pa+Pb=NN> 4
1. ) Сперва, докажемчто для любого натуральногоn⩾ 2, найдётся сумма двух (не обязательно разных) простых чисел, равная, либо превосходящая максимальное значение интервала (от nдо 2n). В ином случае, доказательство гипотезы, не имеет смысла.
Исходя из теоремы Чебышёва.
«Для любого натуральногоn⩾ 2 найдётся простое числоp в интервале
n< p< 2n. »
Делаем вывод, что сумма двух простых (в данном случаем, одинаковых) на интервале от n до 2n, превзойдётмаксимальное значение интервала. Что и требовалось доказать.
т. е.
n< 2p> 2n.
Поскольку речь идёт, о натуральном ряде чисел, (1, 2, 3…),
где разница между двумя ближайшими, соседними членами равна единице (d=1), то это даёт понять нам, что
разница между, любыми, n и p , равна, минимум, единице.
p-n = 1*x
Следовательно,
n=p-1*x .
2n=2p-2x .
2. ) Рассмотрим свойство простых чисел
«Всякое простое число, большее 3, представимо в виде 6 k + 1 {\displaystyle 6k+1} 6k 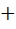 1 (V) или 6 k − 1 {\displaystyle 6k-1} 6k
1 (V) или 6 k − 1 {\displaystyle 6k-1} 6k 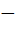 1, где k {\displaystyle k} K— некоторое натуральное число.
1, где k {\displaystyle k} K— некоторое натуральное число.
Отсюда, если разность между несколькими последовательными простыми числами (при k> 1) одинакова, то она обязательно кратна 6. »
Следовательно сумма, таких простых, обязана, также, делиться на 6.
Поскольку, «Всякое простое число, большее 3, представимо в виде 6 k + 1 {\displaystyle 6k+1} 6k 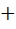 1 (V) или 6 k − 1 {\displaystyle 6k-1} 6k
1 (V) или 6 k − 1 {\displaystyle 6k-1} 6k 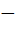 1». Но не каждое число, представленное формулой 6k
1». Но не каждое число, представленное формулой 6k 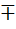 1, является простым.
1, является простым.
Обозначим группу чисел, представленную формулой 6k 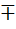 1 Op.
1 Op.
Группа чисел Op. Содержит, как простые, так и составные числа.
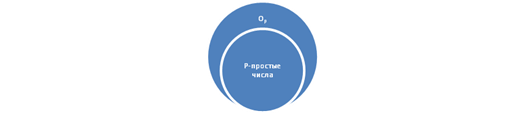
Преобразуем формулу.
Op = 6k 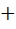 1 V6k
1 V6k 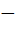 1
1
K= 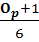 v
v 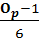
Дабы различать числа, полученные выше представленной формулой, обозначим группы чисел буквами (с и d).
c= 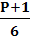 d=
d= 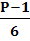
Поскольку свойства группы, распространяется и на частный случай (на простые числа).
3. ) Докажем, что любое чётное число, начиная с 10, можно представить в виде суммы двухчленов, изгрупп чисел Op.
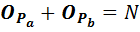 Рассмотрим все варианты сложения членов группы чисел Op (табл, 1. ), для P> 3 иN> 8(табл, 2. ).
Рассмотрим все варианты сложения членов группы чисел Op (табл, 1. ), для P> 3 иN> 8(табл, 2. ).
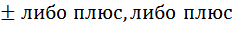
(c+d)= 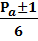 +
+ 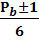
Далее знаменатель в, ниже представленных, формулах, обозначает лишь то, что число кратное 6, а знак 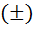 , условия делимости.
, условия делимости.
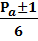 +
+ 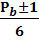 =>
=>  v
v 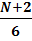 v
v 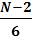
Где 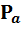 и
и 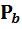 некоторые простые числа.
некоторые простые числа.
(табл, 1. )
| + | 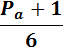
| 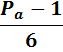
| 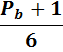
| 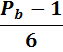
|
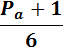
| 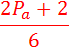
| невозможно | 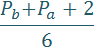
| 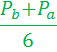
|
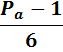
| невозможно | 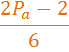
| 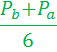
| 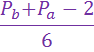
|
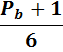
| 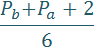
| 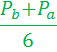
| 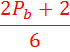
| невозможно |
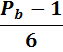
| 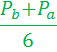
| 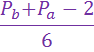
| невозможно | 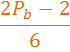
|
Из таблицы (табл, 1. ) видно, что для N, возможны следующие варианты(табл, 2. ).
Для N делающейся на 6, без дополнительных манипуляций, верно следующее утверждение:
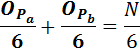
Для N делающейся на 6, лишь с добавлении двойки, верно следующее утверждение
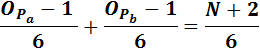
(табл, 2. )
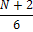
| 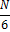
| 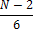
| |
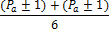
| 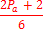
| 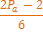
| |
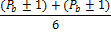
| 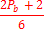
| 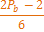
| |
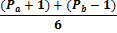
|
| ||
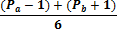
| |||
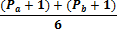
| 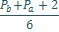
| ||
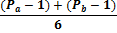
| 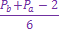
|
Для N делающейся на 6, лишь с вычетом двойки, верно следующее утверждение
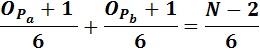
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|